II.
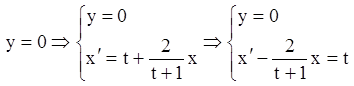 .
(1.27)
.
(1.27)
Розв’язавши лінійні рівняння (1.26) і (1.27) із другого з них одержимо
сімейство особих розв'язків системи. Таким чином, через кожну точку площини ![]() проходить нескінченно багато розв'язків
цієї системи.
проходить нескінченно багато розв'язків
цієї системи.
Інтегралом нормальної системи (1.16) називають
функцію ![]() визначену й неперервну разом зі своїми, що
не звертаються одночасно в нуль в області
визначену й неперервну разом зі своїми, що
не звертаються одночасно в нуль в області ![]() частинними
похідними першого порядку
частинними
похідними першого порядку ![]() ,
, ![]()
![]() , і таку, що повний
диференціал цієї функції звертається тотожно в нуль при підстановці в нього
довільного розв'язання
, і таку, що повний
диференціал цієї функції звертається тотожно в нуль при підстановці в нього
довільного розв'язання ![]() ,
, ![]() , ...,
, ..., ![]() системи
(1.16), тобто:
системи
(1.16), тобто:
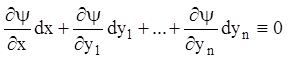 .
(1.28)
.
(1.28)
Помноживши й розділивши на ![]() останню рівність
одержимо:
останню рівність
одержимо:
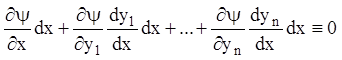 .
.
Розділивши на ![]() одержимо:
одержимо:
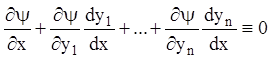 .
.
Тоді в силу (1.16):
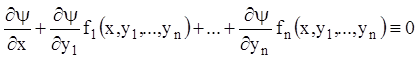 . (1.29)
. (1.29)
З передостанньої тотожності маємо, що повна похідна по ![]() від функції
від функції ![]() тотожно
дорівнює нулю. Тому що:
тотожно
дорівнює нулю. Тому що:
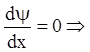
![]() ,
, ![]() .
(1.30)
.
(1.30)
Рівність (1.30), де ![]() – інтеграл системи, а
– інтеграл системи, а ![]() – довільна постійна, називають першим
інтегралом системи. Існування інтеграла системи тісно пов'язане з
існуванням її загального розв'язання. Дійсно, нехай
– довільна постійна, називають першим
інтегралом системи. Існування інтеграла системи тісно пов'язане з
існуванням її загального розв'язання. Дійсно, нехай
![]()
![]() (1.31)
(1.31)
є загальним розв'язанням
системи (1.16). Надаючи постійним ![]() конкретного числового
значення, будемо одержувати часткові розв'язання системи (1.16). Щоб знайти
визначене частинне розв'язання, наприклад, таке, котре задовольняє початковим
умовам (1.17), необхідно визначити
конкретного числового
значення, будемо одержувати часткові розв'язання системи (1.16). Щоб знайти
визначене частинне розв'язання, наприклад, таке, котре задовольняє початковим
умовам (1.17), необхідно визначити ![]() із системи рівнянь
із системи рівнянь
![]()
![]() (1.32)
(1.32)
і підставити, знайдені ![]() в (1.31). На підставі теореми існування й
одиничності розв'язання рівняння (1.32) однозначно розв'яжуться відносно
в (1.31). На підставі теореми існування й
одиничності розв'язання рівняння (1.32) однозначно розв'яжуться відносно ![]() . Виходить, тоді якобіан
. Виходить, тоді якобіан
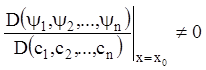 .
(1.33)
.
(1.33)
Звідси робимо висновок, що рівності (1.31) розв'яжуться відносно ![]() (тому що
(тому що ![]() довільне
число), тому будемо мати:
довільне
число), тому будемо мати:
![]()
![]() .
(1.34)
.
(1.34)
Функції ![]() саме і є інтегралами системи
(1.16), тому що по своїй природі вони перетворюються в постійні, коли в них
замість
саме і є інтегралами системи
(1.16), тому що по своїй природі вони перетворюються в постійні, коли в них
замість ![]() підставити розв'язання (1.31) системи
(1.16). Оскільки рівності (1.34) повинні дозволятися відносно
підставити розв'язання (1.31) системи
(1.16). Оскільки рівності (1.34) повинні дозволятися відносно ![]() , тобто
, тобто
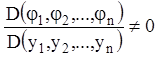 ,
(1.35)
,
(1.35)
те інтеграли ![]() є незалежними. Інакше кажучи, між
функціями
є незалежними. Інакше кажучи, між
функціями ![]() не існує співвідношення
не існує співвідношення
![]() (1.36)
(1.36)
при будь-якому виборі функції
![]() , що явно не залежить від
, що явно не залежить від ![]() . Якби співвідношення (1.36) мали місце, то
не можна було б знайти функції
. Якби співвідношення (1.36) мали місце, то
не можна було б знайти функції ![]() із системи (1.34).
із системи (1.34).
Висновок. Якщо відомо
загальне розв'язання нормальної системи (1.16), то досить його розв'язати щодо
довільних постійних, щоб одержати ![]() незалежних інтегралів
системи.
незалежних інтегралів
системи.
Розглянемо питання про число незалежних інтегралів нормальної системи.
Нехай ![]() – інтеграли системи (1.16). Щодо
них будемо припускати, що вони мають безперервні частинні похідні по
– інтеграли системи (1.16). Щодо
них будемо припускати, що вони мають безперервні частинні похідні по ![]() . Тоді мають місце теореми 1 й 2.
. Тоді мають місце теореми 1 й 2.
Теорема 1. Довільна диференційована функція від будь-якого числа інтегралів нормальної системи (1.16) теж є інтегралом цієї системи.
Доведення.Нехай
![]() , де
, де ![]() – довільна
диференційована функція аргументів
– довільна
диференційована функція аргументів ![]() (інтегралів системи
(1.16)). Тоді, по визначенню інтеграла системи
(інтегралів системи
(1.16)). Тоді, по визначенню інтеграла системи
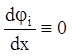
![]() .
(1.37)
.
(1.37)
Але повна похідна функції:
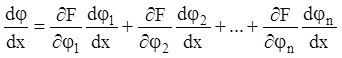 ,
,
і в силу (1.37) 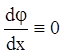 . Тоді
. Тоді ![]() й
функція
й
функція ![]() теж є інтегралом цієї системи, що й було
потрібно довести.
теж є інтегралом цієї системи, що й було
потрібно довести.
Теорема 2. Нормальна система (1.16) може мати не більше чим ![]() незалежних інтегралів.
незалежних інтегралів.
З теореми маємо, що якщо відомі ![]() інтеграл
системи (1.16), те вони залежні між собою. Згадуємо визначення: функції
інтеграл
системи (1.16), те вони залежні між собою. Згадуємо визначення: функції ![]() ,
, ![]() , ...,
, ..., ![]() визначені й неперервні разом з усіма
їхніми частинними похідними 1-го порядку в якійсь
визначені й неперервні разом з усіма
їхніми частинними похідними 1-го порядку в якійсь ![]() -
мірної області
-
мірної області ![]() , називають залежними в
цій області, якщо хоча б одна з них, наприклад,
, називають залежними в
цій області, якщо хоча б одна з них, наприклад, ![]() , є функцією
інших, тобто:
, є функцією
інших, тобто:
![]() .
(1.38)
.
(1.38)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.