Практичне заняття №12
Тема заняття: «Теорія стійкості, основні поняття. Дослідження стійкості лінійних систем»
I. Перевірка виконаного домашнього завдання.
II. Теоретичне опитування:
1. Навіщо при побудові математичної моделі потрібна задача дослідження стійкості?
2. Визначення стійкості розв'язання диференціального рівняння в класичній постановці Ляпунова.
3. Визначення асимптотичної стійкості.
4. Фазова площина, фазова траєкторія й трактування стійкості незбуреного руху.
5. Автономна й неавтономна система, що встановилася й несталий рух.
6. Теорія про стійкість точок спокою ОЛС.
7. Стійкість лінійних автономних систем.
8. Стійкість систем другого порядку. Класифікація точок спокою.
III. Розв'язання задач:
Виходячи з визначення стійкості по Ляпунову з'ясувати, чи стійкі розв'язання даних рівнянь із зазначеними початковими умовами:
1. 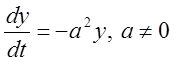 ,
, ![]() ç
ç![]() .
.
Розв'язання: Інтегруючи, знаходимо загальне
розв'язання ![]() . Використовуючи початкові умови, одержуємо
. Використовуючи початкові умови, одержуємо
![]() . Як інше розв'язання візьмемо
. Як інше розв'язання візьмемо ![]() . Тоді для кожного
. Тоді для кожного ![]() з
початкової нерівності
з
початкової нерівності ![]() в нашому випадку
в нашому випадку ![]() повинна випливати оцінка
повинна випливати оцінка ![]() вже для кожного
вже для кожного ![]() .
Ця оцінка, мабуть, має місце, якщо тільки
.
Ця оцінка, мабуть, має місце, якщо тільки ![]() .
Значить розв'язання рівняння стійко. Більш того, тому що
.
Значить розв'язання рівняння стійко. Більш того, тому що 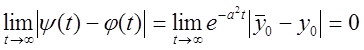 , той досліджуваний рух буде ще й асимптотично
стійким.
, той досліджуваний рух буде ще й асимптотично
стійким.
2. 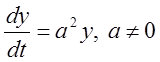 ,
, ![]() ç
ç![]() .
.
Розв'язання: Інтегруючи, одержуємо ![]() . Тоді
. Тоді ![]()
![]() , що з початкової нерівності
, що з початкової нерівності
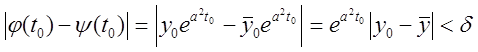
маємо 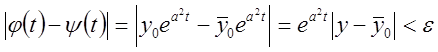 для
для
![]() . Але це неможливо, тому що
. Але це неможливо, тому що ![]() при
при ![]() . Тому
досліджуваний рух нестійкий.
. Тому
досліджуваний рух нестійкий.
3. 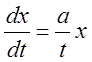 ,
, ![]() . 4.
. 4. 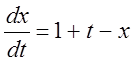 ,
, ![]() . 5.
. 5. 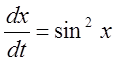 ,
, ![]() . 6.
. 6. 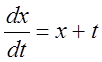 ,
, ![]() . 7.
. 7. 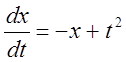 ,
, ![]() .
.
Дослідити на стійкість наступні лінійні системи:
1. ![]() ,
, ![]() .
.
Розв'язання:Складемо фундаментальну матрицю системи
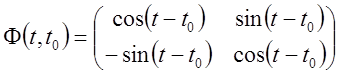 .
.
Ця матриця обмежена, тому що
![]() .
.
Тоді досліджувана система стійка.
2. ![]() ,
, ![]() .
.
Розв'язання: Складемо фундаментальну матрицю ![]() :
:
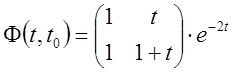 .
.
Тоді 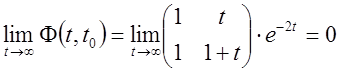 . Тоді досліджувана система
асимптотично стійка.
. Тоді досліджувана система
асимптотично стійка.
3. ![]() ,
, ![]() .
.
Розв'язання: Складемо фундаментальну матрицю ![]() :
:
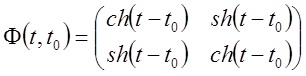 ,
,
тоді
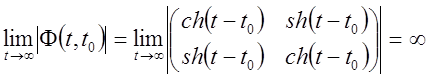 .
.
Тоді досліджувана система нестійка.
4.
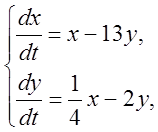
![]() . 5.
. 5. 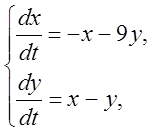
![]() .
.
З'ясувати питання про стійкість точки спокою лінійних автономних систем:
1. ![]() ,
, ![]() .
.
Розв'язання: Складаємо характеристичне рівняння
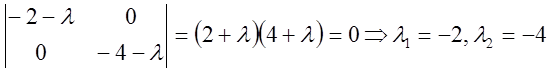 .
.
Тому що обидва характеристичних числа від’ємні, то точка спокою системи
![]() асимптотично стійка.
асимптотично стійка.
2. ![]()
![]() .
.
Розв'язання: Записуємо характеристичне рівняння
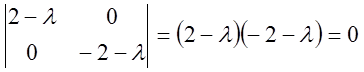 ,
,
звідки одержуємо ![]() ,
, ![]() . Тому
що ці числа протилежних знаків, то точка спокою нестійка.
. Тому
що ці числа протилежних знаків, то точка спокою нестійка.
3. 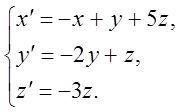 4.
4. 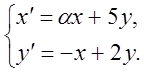 5.
5. 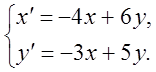
IV. Домашнє завдання:
1. Підготувати теоретичний матеріал по темі «Критерії стійкості: Гурвіца, Л’єнара-Шиппара, Михайлова».
2. Розв’язати вдома задачі, що залишилися.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.