Розглянемо лінійну однорідну систему диференціальних рівнянь
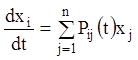
![]() ,
(3.16)
,
(3.16)
стійкість розв'язань якої будемо досліджувати, досліджуючи на стійкість точку спокою системи. Запишемо систему (3.16) у матричному виді
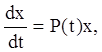 (3.17)
(3.17)
думаючи
 ,
, 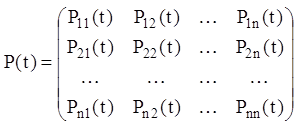 ,
, 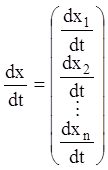 .
.
Якщо матриця P(t) неперервна при ![]() , то з
теореми існування й одиничності маємо, що система (3.17) має єдине розв'язання,
що задовольняє заданим початковим умовам
, то з
теореми існування й одиничності маємо, що система (3.17) має єдине розв'язання,
що задовольняє заданим початковим умовам
![]() ,
(3.18)
,
(3.18)
і єдину нормальну
фундаментальну матрицю ![]() , причому вона не залежить від
початкових умов (3.18) (
, причому вона не залежить від
початкових умов (3.18) (![]() ). При цьому
розв'язання задачі (3.17-3.18) має вигляд
). При цьому
розв'язання задачі (3.17-3.18) має вигляд
![]() . (3.19)
. (3.19)
Звідси маємо, що питання стійкості точки спокою системи однозначно
вирішується за структурою елементів фундаментальної матриці ![]() .
.
Теорема 1. Якщо
при ![]() матриця
матриця ![]() обмежена,
то точка спокою системи (3.16) стійка, якщо
обмежена,
то точка спокою системи (3.16) стійка, якщо ![]() , то
точка спокою системи асимптотично стійка, якщо матриця
, то
точка спокою системи асимптотично стійка, якщо матриця ![]() при
при
![]() не обмежена, то точка спокою нестійка.
не обмежена, то точка спокою нестійка.
Доведення. Виходячи
із властивостей матриці ![]() , розглянемо наступні
випадки:
, розглянемо наступні
випадки:
1) матриця ![]() обмежена при
обмежена при ![]() , тобто
, тобто![]() число
М>0, таке, що
число
М>0, таке, що
 при
при ![]() .
(3.20)
.
(3.20)
Тоді для будь-якого розв'язання ![]() системи
(3.17) при
системи
(3.17) при ![]() вірна нерівність
вірна нерівність
![]() ,
(3.21)
,
(3.21)
у наслідок якої ![]() (3.22) при
(3.22) при ![]() , як
тільки
, як
тільки 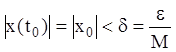 (3.23), тобто розв'язання
(3.23), тобто розв'язання ![]() системи (3.17) стійко. Якщо постійна
системи (3.17) стійко. Якщо постійна ![]() в (3.21) не залежить від
в (3.21) не залежить від ![]() , тобто оцінка (3.22) рівномірна по
, тобто оцінка (3.22) рівномірна по ![]() , тоді точка спокою системи (3.17) рівномірно
стійка.
, тоді точка спокою системи (3.17) рівномірно
стійка.
2) Якщо ![]() , то матриця
, то матриця ![]() обмежена при
обмежена при ![]() , і,
отже, розв'язання
, і,
отже, розв'язання ![]() стійке. Крім того, з (3.19)
маємо, що
стійке. Крім того, з (3.19)
маємо, що ![]() для будь-якого розв'язання
для будь-якого розв'язання ![]() . Тому розглянуте розв'язання
. Тому розглянуте розв'язання ![]() системи рівнянь (3.17) асимптотично
стійке.
системи рівнянь (3.17) асимптотично
стійке.
3) Якщо матриця ![]() необмежена при
необмежена при ![]() , тобто існує така зростаюча числова
послідовність
, тобто існує така зростаюча числова
послідовність ![]() ,
, ![]() ,
, ![]() , що
, що ![]() . Тоді
згідно (3.19) розв'язання буде нестійке, тому що хоча б для одного елемента
. Тоді
згідно (3.19) розв'язання буде нестійке, тому що хоча б для одного елемента ![]() матриці
матриці ![]() виконується
співвідношення
виконується
співвідношення
![]() .
(3.24)
.
(3.24)
Отже, ![]() , а це значить, що точка спокою
системи нестійка.
, а це значить, що точка спокою
системи нестійка.
Можна довести й зворотні твердження. Доведемо, що зі стійкості точки
спокою системи витікає обмеженість матриці ![]() . Тоді,
по визначенню стійкості, для
. Тоді,
по визначенню стійкості, для ![]()
![]() ,
що як тільки
,
що як тільки ![]() , то
, то ![]() при
при ![]() . Тоді, згідно (3.19), при
. Тоді, згідно (3.19), при ![]()
![]() .
(3.25)
.
(3.25)
Звідси маємо, що матриця ![]() обмежена, тому що в
противному випадку існувала б така послідовність
обмежена, тому що в
противному випадку існувала б така послідовність ![]() , що
, що
![]() ,
,
а це суперечить нерівності (3.25).
Якщо точка спокою асимптотично стійка, те![]() ,
звідки згідно (3.19) маємо
,
звідки згідно (3.19) маємо ![]() .
.
Якщо точка спокою нестійка, то матриця ![]() необмежена,
тому що в противному випадку точка спокою була б стійкою.
необмежена,
тому що в противному випадку точка спокою була б стійкою.
Приклад 1. Установити стійкість системи
![]() ,
, ![]() .
.
Розв’язання.Складемо фундаментальну матрицю системи
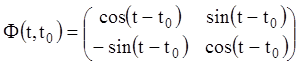 .
.
Ця матриця обмежена, тому що, згідно (3.20)
![]() .
.
Тоді досліджувана система стійка.
Приклад 2. Дослідити стійкість системи
![]() ,
, ![]() .
.
Розв’язування. Складемо фундаментальну матрицю ![]() :
:
 .
.
Тоді 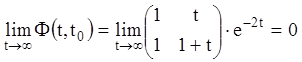 . Тоді досліджувана система
асимптотично стійка.
. Тоді досліджувана система
асимптотично стійка.
Приклад 3. Установити стійкість системи
![]() ,
, ![]() .
.
Розв’язання. Складемо фундаментальну матрицю ![]() :
:
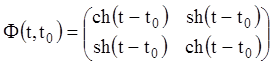 ,
,
тоді
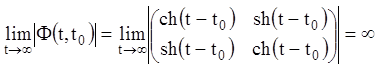 .
.
Тоді досліджувана система нестійка.
У попередньому пункті ми встановили умови стійкості розв'язань лінійних
систем, наклавши обмеження на фундаментальну матрицю. Отримані там критерії
виявляються ефективними тільки в тих випадках, коли така матриця знайдена в
явному виді, наприклад, у випадку лінійних систем з постійними коефіцієнтами. У
цьому випадку матриця ![]() – постійна, і система має
вигляд:
– постійна, і система має
вигляд:
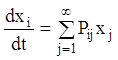
![]() .
(3.26)
.
(3.26)
З теорії систем лінійних диференціальних рівнянь із постійними коефіцієнтами відомо, що фундаментальна система розв'язань такої системи завжди може бути побудована з елементарних функцій, При цьому частинне розв'язання системи шукаємо у вигляді
![]()
![]() ,
, ![]() .
.
Характеристичні числа ![]() є коріннями
характеристичного рівняння
є коріннями
характеристичного рівняння
![]() .
(3.27)
.
(3.27)
Розглянемо окремі випадки.
1) Всі корені характеристичного рівняння (3.27) мають від’ємні дійсні частини (тобто або дійсних корені від’ємні, або комплексні корені мають від’ємну дійсну частину).
Якщо покласти, що всі корені ![]() дійсні, різні й
від’ємні, то всі розв'язання
дійсні, різні й
від’ємні, то всі розв'язання ![]() прагнуть до нуля при
прагнуть до нуля при ![]() , тобто
, тобто
![]() .
.
Якщо
![]() ,
, ![]() , то, з
огляду на що
, то, з
огляду на що
![]() ,
,
то ![]() (тому
що
(тому
що ![]() ).
).
Якщо ![]() є від’ємним коренем кратності
є від’ємним коренем кратності ![]() , то йому відповідають розв'язання
, то йому відповідають розв'язання
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.