Дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами

ЛЕКЦИЯ №10.

Тема: 10. Дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами

ПЛАН

10.1 Дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами

10.1.1 Линейное уравнение Эйлера

10.1.2 Линейное уравнение Лагранжа

10.1.3 Уравнение Чебышева

10.2 Интегрирование дифференциальных уравнений при помощи степенных рядов

10.1 Дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами

Так как однородное линейное уравнение с постоянными коэффициентами всегда интегрируются в элементарных функциях, то можно поставить задачу о возможности приведения однородного линейного уравнения с переменными коэффициентами к уравнению с постоянными коэффициентами при помощи замены независимой переменной или искомой функции.

Пусть задано ОЛДУ

.        (10.1)

Попробуем привести это уравнение к ЛОДУ с постоянными коэффициентами при помощи замены независимой переменной. Сделаем подстановку:

.                              (10.2)

Тогда:

и после подстановки уравнение (10.1) преобразуем к виду:

.

Разделив на , получаем:

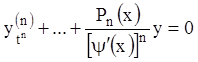.                      (10.3)

Отсюда ясно, что функцию  необходимо выбрать так, чтобы коэффициент при  в уравнение (10.3) был постоянным.

Положим 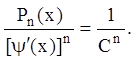 Тогда , откуда:

.

Таким образом, если уравнение (10.1) приводимо к уравнению с постоянными коэффициентами при помощи замены независимой переменной, то только по формуле вида:

                     (10.4)

В качестве примеров применения подстановки (10.4) рассмотрим следующие  уравнения.

10.1.1 Линейное уравнение Эйлера

Уравнение вида:

,  (10.5)

где  называют линейным уравнением Эйлера.

Разрешая это уравнение относительно , видим, что точка  является особой точкой уравнения. Но условия теоремы существования и единственности выполнены в каждом из интервалов  и .

Сравнивая уравнение Эйлера с уравнением (10.1), мы видим, что 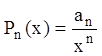. Поэтому, по формуле (10.4),

.

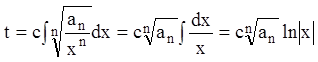Полагая  и опуская постоянную интегрирования, получаем  или

.                                (10.6)

Тогда:

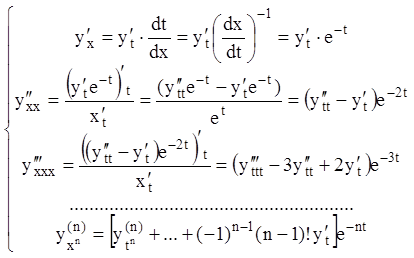.            (10.7)

Из (10.7) видим, что производная -го порядка от по   выражается в виде произведения  на однородную линейную функцию от  с постоянными коэффициентами. Поэтому подставляя (10.6) и (10.7) в (10.5) и замечая, что множители  взаимно уничтожаются с множителями , мы получаем однородное линейное уравнение -го порядка с постоянными коэффициентами:

.                 (10.8)

Найдя общее решение этого уравнения и осуществив обратную замену , получим общее решение уравнения Эйлера.

Общее решение уравнения (10.5) было известно и Бернулли в 1700 г. Эйлер исследовал это уравнение в 1740 г. и в 1769 г. опубликовал свои результаты. Позднее этим уравнением занимался О. Коши.

Так как частное решение уравнения (10.8) приходится искать в виде , то, не приводя уравнение (10.5) к виду (10.8), следует (на практике всегда так и делается) искать его в виде:

.                                  (10.9)

Тогда простому корню характеристического уравнения, например , будет соответствовать решение , а кратному –

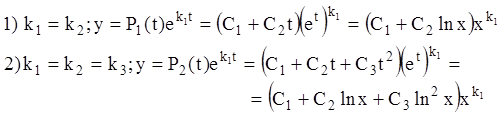 (10.10)

П р и м е р  1. Найти общее решение уравнения:

.

Р е ш е н и е. Ищем частное решение в виде .

Тогда  Подставим в уравнение

.

Значит общее решение:

.

П р и м е р  2. .

Р е ш е н и е. Частное решение ищем в виде . Тогда  Подставим в уравнение ;

, .

В случае комплексных и различных корней характеристические уравнения  функции

 и

будут вещественными решениями, и в формуле общего решения им соответствует выражение

.            (10.11)

П р и м е р  3. .

Р е ш е н и е.

,

. Тогда из (10.11):

.

 Можно показать, что если  кратные корни характеристического уравнения кратности , то в формуле общего решения им соответствует выражение:

,        (10.12)

где- многочлены степени () с произвольными коэффициентами  

П р и м е р  4. .

Р е ш е н и е. Частное решение ищем в виде .

Тогда:

Подставляем в уравнение

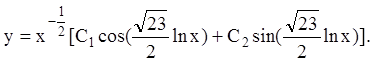
Если уравнение Эйлера неоднородное, то для нахождения его общего решения принимаются изложенные выше методы.

П р и м е р  5. .

Р е ш е н и е. , . Замена  

 

Частное решение ищем в виде: .

Тогда  Подставим в уравнение, получаем:  

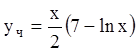. Тогда общее решение неоднородного уравнения:

З а м е ч а н и е. При решении уравнения Эйлера на интервале  производится замена .

10.1.2 Линейное уравнение Лагранжа

Линейным уравнением Лагранжа называют уравнение вида:

,                 (10.13)

где  и  - постоянные. Подстановкой

                            (10.14)

уравнение Лагранжа приводится к линейному уравнению с постоянными коэффициентами.