П р и м е р 1. Найти решение в виде степенного ряда уравнения:
![]() . (10.23)
. (10.23)
Р е ш е н и е. Решение этого
уравнения в элементарных функциях имеет вид: ![]() . Будем
искать решение
. Будем
искать решение ![]() в виде степенного ряда
в виде степенного ряда
![]() . (10.24)
. (10.24)
Покажем, что ряд (10.24)
сходящийся и дважды дифференцируемый (условия теоремы существования выполнены).
Вычислим ![]() и
и ![]() :
:
 .
(10.25)
.
(10.25)
Подставляя (10.24) и (10.25) в уравнение (10.23), получаем тождество:

Так как сходящиеся степенные ряды являются абсолютно сходящимися внутри интервала сходимости, предыдущее равенство можно привести к виду:
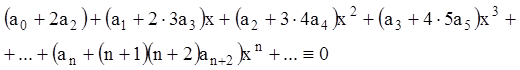 .
(10.26)
.
(10.26)
Отсюда следует, что все коэффициенты ряда (10.26) равны нулю, т.е.:
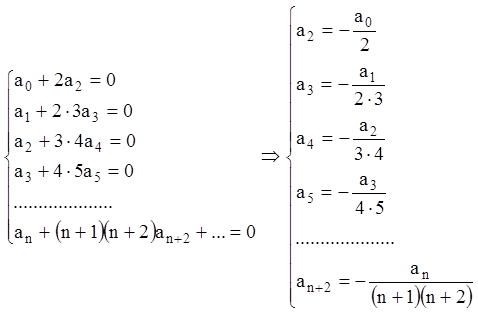 .
.
Т.о., оставляя произвольными ![]() и
и ![]() (они не
определяются из этих уравнений), будем иметь:
(они не
определяются из этих уравнений), будем иметь:
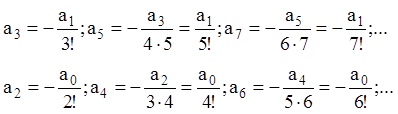 .
.
Подставляя найденные значения
коэффициентов в (10.24) и группируя члены с ![]() и
и ![]() , получаем:
, получаем:
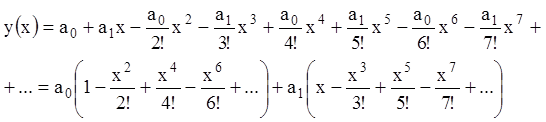 .(10.27)
.(10.27)
Очевидно, что ряды, стоящие в
скобках равномерно сходящиеся при ![]() , производные этих
рядов тоже равномерно сходятся на том же интервале. Учитывая, что:
, производные этих
рядов тоже равномерно сходятся на том же интервале. Учитывая, что:

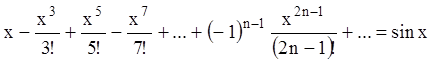
получаем известное решение:
![]() .
.
Применяя ряды, мы, по сути, ищем частные решения дифференциального уравнения, но в виде ряда.
П р и м е р 2. Найти частное решение дифференциального уравнения:
![]() , (10.28)
, (10.28)
если:
![]() (10.29)
(10.29)
Р е ш е н и е. Решение ![]() ищем в виде ряда:
ищем в виде ряда:
![]() . (10.30)
. (10.30)
Из (10.30) с учетом (10.29), получаем
![]() . Дифференцируем (10.30) и используем
(10.29), получаем:
. Дифференцируем (10.30) и используем
(10.29), получаем:
![]() . (10.31)
. (10.31)
![]() . Из
(10.31), получаем:
. Из
(10.31), получаем:
![]() . (10.32)
. (10.32)
Подставим (10.32) и (10.30) в
(10.28) и, приравнивая коэффициенты при одинаковых степенях ![]() в левой и правой части, получаем:
в левой и правой части, получаем:
![]()
![]()
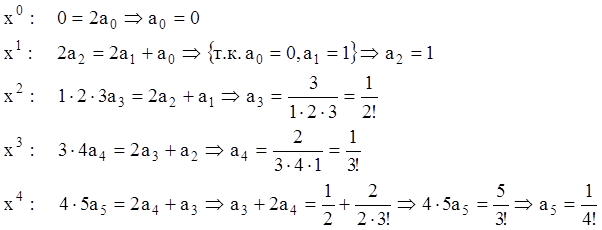
Аналогично: 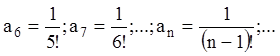
![]()

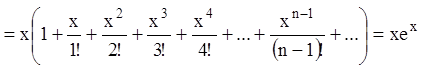 .
.
П р и м е р 3. Решить уравнение:
![]() , (10.33)
, (10.33)
где ![]() .
Это уравнение называют уравнением Бесселя порядка
.
Это уравнение называют уравнением Бесселя порядка ![]() , хотя
впервые его получили и нашли решение в виде ряда Д. Бернулли и Л. Эйлер. К
этому уравнению приводятся многие задачи физики, механики и астрономии.
, хотя
впервые его получили и нашли решение в виде ряда Д. Бернулли и Л. Эйлер. К
этому уравнению приводятся многие задачи физики, механики и астрономии.
Решение уравнения (10.33) будем искать в виде так называемого обобщенного степенного ряда:
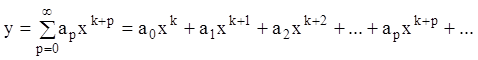 , (10.34)
, (10.34)
где ![]() не
целое число, которое надо определить. Полагаем, что ряд (10.34) является
решением уравнения (10.33), значит, он сходящийся и дважды дифференцируемый,
будем иметь:
не
целое число, которое надо определить. Полагаем, что ряд (10.34) является
решением уравнения (10.33), значит, он сходящийся и дважды дифференцируемый,
будем иметь:
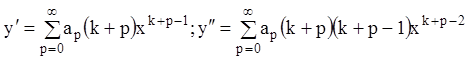 . (10.35)
. (10.35)
Подставив (10.35) и (10.34) в (10.33), получаем:

 или
или
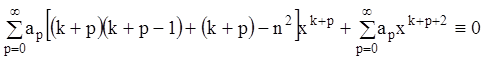 или
или  .
.
Забрав из первой суммы два первых слагаемых, последнее тождество можно записать в виде:
![]()
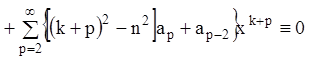 . (10.36)
. (10.36)
В связи с неопределенностью
степени ![]() можно положить
можно положить ![]() . Тогда
тождество (10.36) будет иметь место при условии, что
. Тогда
тождество (10.36) будет иметь место при условии, что
![]() , (10.37)
, (10.37)
![]() , (10.38)
, (10.38)
![]() . (10.39)
. (10.39)
Уравнение (10.37) называют определяющим
уравнением. Из него имеем ![]() или
или ![]() . Подставляя в (10.38)
. Подставляя в (10.38) ![]() , получим:
, получим:
![]() .
.
Далее из (10.39) будем иметь
(при ![]() ):
):
 ,
,
при ![]() :
:
![]()
и вообще ![]() .
Значит, все коэффициенты с нечетным индексом являются нулями, а с четным индексом
–
.
Значит, все коэффициенты с нечетным индексом являются нулями, а с четным индексом
–
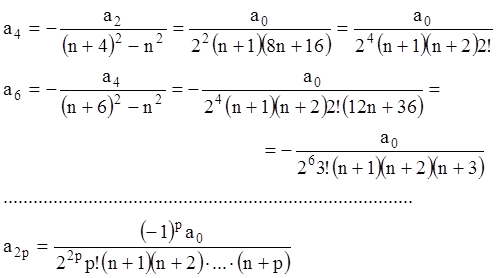 .
.
Подставив найденные значения коэффициентов в (10.34), подучим одно частное решение уравнения (10.33):
 ,
,
где ![]() –
произвольная постоянная. Этому решению можно придать более удобный вид, если
выбрать произвольное постоянное
–
произвольная постоянная. Этому решению можно придать более удобный вид, если
выбрать произвольное постоянное 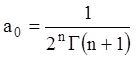 , где
, где ![]() – гамма-функция Эйлера, определяемая как
несобственный интеграл:
– гамма-функция Эйлера, определяемая как
несобственный интеграл:
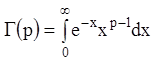 , при
любом
, при
любом ![]() .
.
Эта функция обладает
свойством ![]() . Эта формула, повторно примененная, дает
. Эта формула, повторно примененная, дает ![]() . Учитывая, что
. Учитывая, что ![]() , в
случае натурального
, в
случае натурального ![]() , получаем:
, получаем:
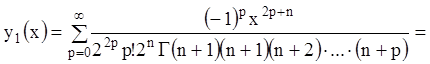
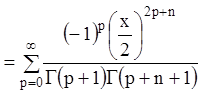 . (10.40)
. (10.40)
Это частное решение (10.40)
обычно обозначается ![]() и называется функцией Бесселя
первого рода порядка
и называется функцией Бесселя
первого рода порядка![]() .
.
Аналогично, при ![]() , выбираем
, выбираем  ,
получаем функцию Бесселя первого рода порядка
,
получаем функцию Бесселя первого рода порядка![]() :
:
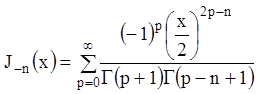 . (10.41)
. (10.41)
Ряды (10.40) и (10.41)
сходятся при любых значениях ![]() (в (10.41)
(в (10.41) ![]() ) и допускают двукратное почленное дифференцирование,
следовательно,
) и допускают двукратное почленное дифференцирование,
следовательно, ![]() и
и ![]() являются
решением уравнения Бесселя.
являются
решением уравнения Бесселя.
При ![]() ,не равном целому числу, решения
,не равном целому числу, решения ![]() и
и ![]() , очевидно, линейно независимые, так как их
разложения в ряды начинаются с различных степеней
, очевидно, линейно независимые, так как их
разложения в ряды начинаются с различных степеней ![]() и,
следовательно, линейная комбинация
и,
следовательно, линейная комбинация ![]() тождественно равна
нулю лишь при
тождественно равна
нулю лишь при ![]() . Тогда общее решение уравнения
Бесселя при
. Тогда общее решение уравнения
Бесселя при ![]() , не равном целому числу, запишется:
, не равном целому числу, запишется:
![]() , (10.42)
, (10.42)
где ![]() и
и
![]() находятся по формулам (10.40) и (10.41).
находятся по формулам (10.40) и (10.41).
При ![]() равном
целому числу функции
равном
целому числу функции ![]() и
и![]() линейно зависимые, т.к.
линейно зависимые, т.к.![]() и вместо
и вместо ![]() выбирают
другое линейно независимое решение – так называемую функцию Бесселя второго
рода
выбирают
другое линейно независимое решение – так называемую функцию Бесселя второго
рода![]() , определяемую как:
, определяемую как:
 ,
,
( ![]() , где
, где ![]() не целое число,
не целое число, ![]() –
целое). Тогда при
–
целое). Тогда при ![]() равном целому числу, общее
решение запишется:
равном целому числу, общее
решение запишется:
![]() ,
,
где ![]() и
и
![]() – произвольные постоянные.
– произвольные постоянные.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.