В самом деле, по
формуле (10.4) 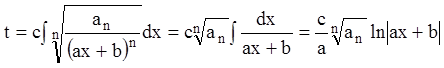 . Полагая
. Полагая 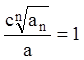 ,
получаем
,
получаем ![]() или
или ![]() , если
, если ![]() и
и ![]() , если
, если ![]() .
.
З а м е ч а н и е 1.
Учитывая, что частные решения полученного уравнения с постоянными
коэффициентами ищем в виде ![]() и
и ![]() , то замена
, то замена ![]() сразу
дает возможность получить характеристическое уравнение.
сразу
дает возможность получить характеристическое уравнение.
З а м е ч а н и е 2. Замена ![]() уравнения Лагранжа приводится к уравнению
Эйлера:
уравнения Лагранжа приводится к уравнению
Эйлера:
![]() ,
,
которое рассмотрено в предыдущем пункте.
П р и м е р 6. Решить уравнение ![]() . Это
уравнение Лагранжа, следовательно, имеет место подстановка
. Это
уравнение Лагранжа, следовательно, имеет место подстановка ![]() . Тогда
. Тогда 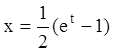 и
и 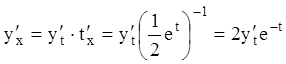 ,
, 
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,следовательно,
,следовательно, ![]() т.к.
т.к.
![]() и
и ![]() , то
, то ![]() . Итого ответ:
. Итого ответ:
![]() .
.
П р и м е р 7. ![]() .
.
Р е ш е н и е.![]() .
.
Подстановка: ![]() ;
; 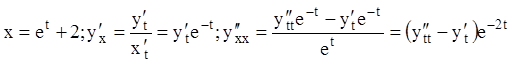 .
.
Подставляем в уравнение ![]() ,
, ![]() ;
; ![]() , т.к.
, т.к. ![]()
![]() .
. ![]() .
Тогда:
.
Тогда: ![]() ,
, 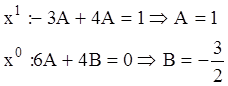 .
.
Ответ: 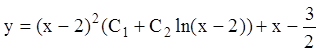 .
.
Уравнение Чебышева – это уравнение вида:
![]() . (10.15)
. (10.15)
Точки ![]() и
и ![]() являются особыми точками этого уравнения.
В каждом из интервалов
являются особыми точками этого уравнения.
В каждом из интервалов ![]() выполнены условия
теоремы существования и единственности.
выполнены условия
теоремы существования и единственности.
Построим общее решение уравнения (10.15) при ![]() . Из формулы (10.4) получаем:
. Из формулы (10.4) получаем:
 . (10.16)
. (10.16)
Полагая 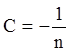 и опуская постоянную интегрирования, получаем:
и опуская постоянную интегрирования, получаем:
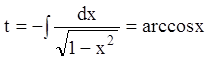 или
или ![]() , или
, или ![]() . (10.17)
. (10.17)
В силу подстановки получаем:
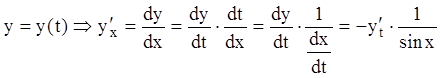 ;
;
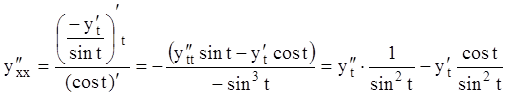 .
.
Подставляя ![]() в (10.15) и заменяя x на
в (10.15) и заменяя x на ![]() , получаем:
, получаем:
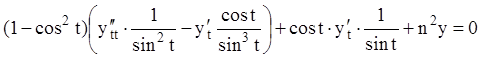 ;
;
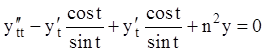 или
или ![]() . (10.18)
. (10.18)
Решаем однородное уравнение: ![]() ,
, ![]()
![]() т.к.
т.к. ![]() , то
, то
![]() . (10.19)
. (10.19)
П р и м е р 8. Решить уравнение: ![]() .
.
Р е ш е н и е. По формуле (10.19) общее решение запишется:
![]() .
.
З а м е ч а н и е 1. При ![]() проводим замену
проводим замену ![]() (
(![]() при
при ![]() и
и ![]() , при
, при ![]() ). Общее
решение в этом случае:
). Общее
решение в этом случае: ![]() .
.
З а м е ч а н и е 2. Иногда линейная замена искомой функции тоже может привести уравнение (10.1) к уравнению с постоянными коэффициентами. В частности, для этой цели используют подстановку
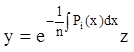 , (10.20)
, (10.20)
которая приводит уравнение (10.1) к
уравнению, не содержащему члена с производной ![]() -го порядка.
-го порядка.
Решение дифференциального
уравнения только в отдельных случаях удается выразить через элементарные
функции или их первообразные. В то же время нам известно, что при наличии
определенных условий любая функция ![]() может быть представлена
в виде степенного ряда. Поэтому вполне естественно, зная, что решение
дифференциального уравнения существует (теорема существования это гарантирует)
ставить вопрос о нахождении его в виде степенного ряда.
может быть представлена
в виде степенного ряда. Поэтому вполне естественно, зная, что решение
дифференциального уравнения существует (теорема существования это гарантирует)
ставить вопрос о нахождении его в виде степенного ряда.
Условия, при которых существуют решения в виде суммы степенного ряда или обобщенного степенного ряда, обычно устанавливаются методами теории функций комплексного переменного, поэтому основные теоремы этого параграфа дадим без доказательства в применении к наиболее часто встречающимся в приложениях уравнениям второго порядка.
Т е о р е м а ( о б а н а л
и т и ч н о с т и р е ш е н и я ). Если ![]() являются
аналитическими функциями
являются
аналитическими функциями ![]() в окрестности точки
в окрестности точки ![]() и
и ![]() , то
решения уравнения:
, то
решения уравнения:
![]() (10.21)
(10.21)
также являются аналитическими функциями в некоторой окрестности той же точки и, следовательно, решения уравнения (10.21) можно искать в виде
![]()
Т е о р е м а ( о р а з л о ж и м о с т и р е ш е н и я в о б о б щ е н –
н ы й с т е п е н н о й р я д ). Если
уравнение (10.21) удовлетворяет условиям предыдущей теоремы, но ![]() является нулем конечного порядка
является нулем конечного порядка ![]() функции
функции ![]() , нулем
порядка
, нулем
порядка ![]() или выше функции
или выше функции ![]() ,
(если
,
(если ![]() ) и нулем порядка не ниже
) и нулем порядка не ниже ![]() коэффициента
коэффициента ![]() (если
(если ![]() ), то существует, по крайней мере, одно
нетривиальное решение уравнения (1’) в виде суммы обобщенного степенного ряда
), то существует, по крайней мере, одно
нетривиальное решение уравнения (1’) в виде суммы обобщенного степенного ряда
![]()
![]() ,
(10.22)
,
(10.22)
где ![]() - некоторое действительное число, которое
может быть как целым, так и дробным, как положительным, так и отрицательным.
- некоторое действительное число, которое
может быть как целым, так и дробным, как положительным, так и отрицательным.
Второе линейно независимое
с (10.22) решение, как правило, имеет тоже вид суммы обобщенного степенного
ряда, но иногда может еще содержать произведение обобщенного степенного ряда на
![]() .
.
При решении же конкретных
задач можно обойтись без сформулированных выше двух теорем, тем более, что эти
теоремы в указанной формулировке все равно не устанавливают области сходимости
рассматриваемых рядов. Чаще всего в конкретных задачах подбирают степенной или
обобщенный степенной ряд, формально удовлетворяющий дифференциальному
уравнению, то есть при подстановке обращающий степенной ряд рассматриваемое
уравнение в тождество, если предполагать сходимость ряда и возможность
почленного дифференцирования ![]() раз. В той области, где
ряд сходится и допускает
раз. В той области, где
ряд сходится и допускает ![]() - кратное почленное
дифференцирование, но не только формально удовлетворяет уравнению, то его сумма
действительно является искомым решением.
- кратное почленное
дифференцирование, но не только формально удовлетворяет уравнению, то его сумма
действительно является искомым решением.
Проиллюстрируем этот метод на конкретных дифференциальных уравнениях второго порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.