де ![]() –
многочлен степеня не вище чим
–
многочлен степеня не вище чим ![]() й
й ![]() , (тому що
, (тому що ![]() й показовій
функції зростає швидше, ніж степенева).
й показовій
функції зростає швидше, ніж степенева).
Аналогічний результат одержуємо у випадку кратних комплексних коренів із від’ємною дійсною частиною.
Із усього
розглянутого, робимо висновок, що нульове розв'язання ![]() системи
(3.26) асимптотично стійке.
системи
(3.26) асимптотично стійке.
2) Характеристичне рівняння (3.28) має корінь із додатними дійсними частинами. Тоді хоча б одна з функцій
![]() ,
,
у якої ![]() буде необмежено зростаючої по модулі при
буде необмежено зростаючої по модулі при ![]() , і тому що вона ввійде до складу одного з
доданків загального розв'язання, то останнє теж необмежено зростає при
, і тому що вона ввійде до складу одного з
доданків загального розв'язання, то останнє теж необмежено зростає при ![]() . Значить нульове розв'язання системи нестійке.
. Значить нульове розв'язання системи нестійке.
3) Характеристичне рівняння не має корінь із від’ємними дійсними частинами, але є простий корінь із дійсною частиною рівною нулю.
У цьому випадку всі
функції ![]() будуть обмежені по модулі для будь-якого
будуть обмежені по модулі для будь-якого ![]() , які б ні були початкові значення цих
функцій. Виходить, при кожному
, які б ні були початкові значення цих
функцій. Виходить, при кожному ![]() найдеться таке
найдеться таке ![]() , що при
, що при ![]() треба
треба ![]() для
для ![]()
![]() ,
, ![]() .
Виходить, нульове розв'язання системи буде стійким, але не буде асимптотично
стійким, тому що в цьому випадку
.
Виходить, нульове розв'язання системи буде стійким, але не буде асимптотично
стійким, тому що в цьому випадку ![]() для всіх
для всіх ![]() .
.
В випадку якщо характеристичне рівняння (3.27), не має корінь із від’ємними дійсними частинами, має кратний корінь, дійсні частини якого дорівнюють нулю, то в цьому випадку розв'язання може бути нестійким, тому що
![]() при
при ![]() ,
,
якщо існують ![]()
![]() .
.
З урахуванням цих досліджень сформулюємо основні теореми про стійкість автономних лінійних систем.
Теорема 1. Якщо
дійсні частини всіх коренів характеристичного рівняння системи від’ємні, ![]() , то незбурений рух (тривіальне
розв'язання) системи (3.26) асимптотично стійкий.
, то незбурений рух (тривіальне
розв'язання) системи (3.26) асимптотично стійкий.
Теорема 2. Якщо серед коренів характеристичного рівняння є хоча б один, дійсна частина якого від’ємна, то незбурений рух (тривіальне розв'язання) системи нестійке.
Теорема 3. Якщо дійсні частини деяких простих коренів характеристичного рівняння дорівнюють нулю, а інші – від’ємні, то незбурений рух стійкий (але не асимптотично).
Приклад 1. Нехай рух деякого об'єкта описується нормальною системою трьох рівнянь, що приводиться до диференціального рівняння
![]() .
.
Відповідне характеристичне рівняння
![]()
має корені ![]()
![]() . Тоді по теоремі 2,
досліджуваний рух нестійкий.
. Тоді по теоремі 2,
досліджуваний рух нестійкий.
Розглянемо важливий окремий випадок лінійної автономної системи 2-го порядку:
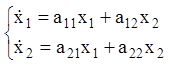 .
(3.28)
.
(3.28)
Дослідимо на стійкість нульове розв'язання системи
![]() ,
, ![]() ,
,
припускаючи, що точка рівноваги ізольована. Частинне розв’язання шукаємо у вигляді
![]() ,
, ![]() , (3.29)
, (3.29)
де ![]() –
постійні. Знаходимо корені характеристичного рівняння
–
постійні. Знаходимо корені характеристичного рівняння
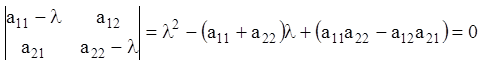 . (3.30)
. (3.30)
Розглянемо різні випадки коренів характеристичного рівняння.
I. Серед коренів характеристичного рівняння немає коренів рівних нулю. Розглянемо можливі в цьому випадку варіанти розв'язань.
1).
Корені дійсні й різні ![]() .
.
Підставивши в (3.29) замість ![]() значення
значення ![]() , а замість
, а замість ![]() і
і ![]() відповідні розв'язання
відповідні розв'язання ![]() й
й ![]() системи
системи
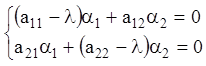 ,
(3.31)
,
(3.31)
одержимо перше розв'язання системи (3.28):
![]() ,
, ![]() .
.
Аналогічно, використовуючи ![]() , одержуємо друге
розв'язання системи:
, одержуємо друге
розв'язання системи:
![]() ,
, ![]() .
.
Загальне розв'язання системи в розглянутому випадку має вигляд
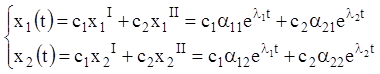 , (3.32)
, (3.32)
де ![]() й
й
![]() – довільні постійні. Вид фазових
траєкторій
– довільні постійні. Вид фазових
траєкторій ![]() в околиці точки рівноваги
в околиці точки рівноваги ![]() буде істотно залежати від знаків
характеристичних чисел. Розглянемо різні варіанти цих знаків.
буде істотно залежати від знаків
характеристичних чисел. Розглянемо різні варіанти цих знаків.
а) Якщо ![]() , то з (3.32), очевидно, що точка
спокою
, то з (3.32), очевидно, що точка
спокою ![]() асимптотично стійка (теорема 1). Всі
фазові траєкторії в розглянутому випадку проходять через точку рівноваги, що у
цьому випадку називається стійким вузлом (всі фазові траєкторії
проходять через точку рівноваги й точка, що зображує, із часом прагне до точки
рівноваги).
асимптотично стійка (теорема 1). Всі
фазові траєкторії в розглянутому випадку проходять через точку рівноваги, що у
цьому випадку називається стійким вузлом (всі фазові траєкторії
проходять через точку рівноваги й точка, що зображує, із часом прагне до точки
рівноваги).
Приклад 1. Дослідити стійкість системи
![]() ,
, ![]() .
.
Розв’язання. Складаємо характеристичне рівняння
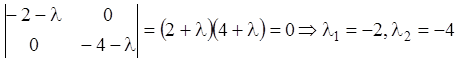 .
.
Тому що обидва характеристичних числа від’ємні, то точка спокою системи
![]() асимптотично стійка.
асимптотично стійка.
 Для
наочності побудуємо фазові траєкторії в околиці точки спокою. Відразу інтегруючи
рівняння даної системи (вони не залежать друг від друга), одержуємо
параметричні рівняння цих траєкторій у вигляді
Для
наочності побудуємо фазові траєкторії в околиці точки спокою. Відразу інтегруючи
рівняння даної системи (вони не залежать друг від друга), одержуємо
параметричні рівняння цих траєкторій у вигляді ![]()
![]() . З параметричних одержуємо звичайне
рівняння фазових траєкторій
. З параметричних одержуємо звичайне
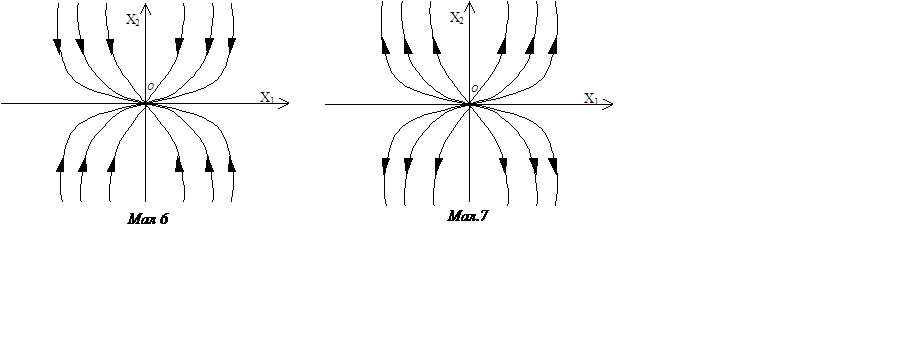
рівняння фазових траєкторій ![]() (сімейство парабол з
вершиною на початку координат, симетричних відносно
(сімейство парабол з
вершиною на початку координат, симетричних відносно ![]() (мал.
6)). Стрілками зазначений напрямок руху по траєкторіях при зростанні
(мал.
6)). Стрілками зазначений напрямок руху по траєкторіях при зростанні ![]() . Точка рівноваги
. Точка рівноваги ![]() –
стійкий вузол.
–
стійкий вузол.
б) Якщо ![]() й
й ![]() , те
, те ![]() при
при ![]() .
Траєкторії аналогічні попередньої, але рух у них буде відбуватися в протилежних
напрямках (точка із часом віддаляється від точки рівноваги). Така точка
рівноваги називається нестійким вузлом (мал. 7).
.
Траєкторії аналогічні попередньої, але рух у них буде відбуватися в протилежних
напрямках (точка із часом віддаляється від точки рівноваги). Така точка
рівноваги називається нестійким вузлом (мал. 7).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.