в) Якщо ![]()
![]() (або
навпаки), то точка спокою теж нестійка, тому що одна з експонент
(або
навпаки), то точка спокою теж нестійка, тому що одна з експонент ![]() при
при ![]() . Однак,
у цьому випадку існує одна траєкторія, по якій рух відбувається в напрямку
початку координат. А, саме, поклавши в (3.32)
. Однак,
у цьому випадку існує одна траєкторія, по якій рух відбувається в напрямку
початку координат. А, саме, поклавши в (3.32) ![]() ,
одержуємо
,
одержуємо
![]() ,
, ![]() .
.
 При різних значеннях
При різних значеннях ![]() одержуємо різні рухи по
однієї й тій же прямій
одержуємо різні рухи по
однієї й тій же прямій 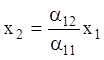 .
.
При зростанні ![]() точки на цій прямій рухаються
по напрямку до початку координат.
точки на цій прямій рухаються
по напрямку до початку координат.
Якщо ![]() , те
, те![]() ,
, ![]() . Точки цієї траєкторії рухаються зі
зростанням
. Точки цієї траєкторії рухаються зі
зростанням ![]() по прямій
по прямій 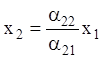 ,
віддаляючись від початку координат. У загальному випадку при
,
віддаляючись від початку координат. У загальному випадку при ![]() й
й ![]() при
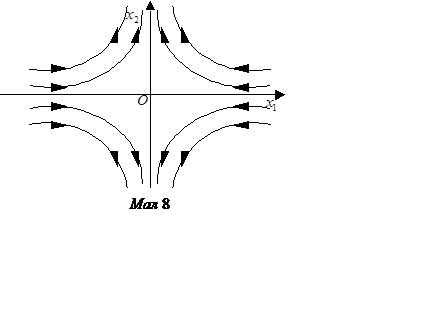
при ![]() траєкторія залишає точку спокою. Точка
спокою цього типу називається сідлом (мал. 8). Характер фазових
траєкторій в околиці сідла з'ясуємо на прикладі.
траєкторія залишає точку спокою. Точка
спокою цього типу називається сідлом (мал. 8). Характер фазових
траєкторій в околиці сідла з'ясуємо на прикладі.
Приклад 2. Дослідити стійкість системи
![]()
![]() .
.
Розв’язання. Записуємо характеристичне рівняння
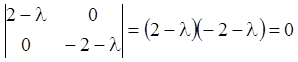 ,
,
звідки одержуємо ![]() ,
, ![]() . Тому
що ці числа протилежних знаків, то точка спокою нестійка. Побудуємо фазові
траєкторії в околиці точки рівноваги. Розділивши друге рівняння на перше,
одержимо диференціальне рівняння фазових траєкторій
. Тому
що ці числа протилежних знаків, то точка спокою нестійка. Побудуємо фазові
траєкторії в околиці точки рівноваги. Розділивши друге рівняння на перше,
одержимо диференціальне рівняння фазових траєкторій
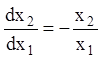 .
.
Розділяючи змінні й інтегруючи, одержуємо ![]() . Це
рівнобічні гіперболи. Стрілками (мал. 7) показаний напрямок руху по цих
траєкторіях точки, що зображує, зі зростанням
. Це
рівнобічні гіперболи. Стрілками (мал. 7) показаний напрямок руху по цих
траєкторіях точки, що зображує, зі зростанням ![]() .
.
2) Корені характеристичного рівняння комплексно-сполучені: ![]() . Загальне розв'язання можна зберегти у
вигляді (3.32), однак, з огляду на те, що його дійсна й мнима частини теж є
розв'язаннями системи (3.28), її загальне розв'язання можна записати у вигляді
лінійної комбінації цих частин:
. Загальне розв'язання можна зберегти у
вигляді (3.32), однак, з огляду на те, що його дійсна й мнима частини теж є
розв'язаннями системи (3.28), її загальне розв'язання можна записати у вигляді
лінійної комбінації цих частин:
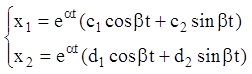 ,
(3.33)
,
(3.33)
![]() зв'язано
один з одним лінійними залежностями.
зв'язано
один з одним лінійними залежностями.
 а)
Якщо
а)
Якщо ![]() , то
, то ![]() при
при ![]() . Отже,
. Отже, ![]() і
і ![]() при
при ![]() ,
залишаючись коливальними функціями з нескінченно убутною амплітудою. Незбурений
рух асимптотично стійкий. Точка, що зображена, у цьому випадку рухається по
спіралі, наближаючись до точки
,
залишаючись коливальними функціями з нескінченно убутною амплітудою. Незбурений
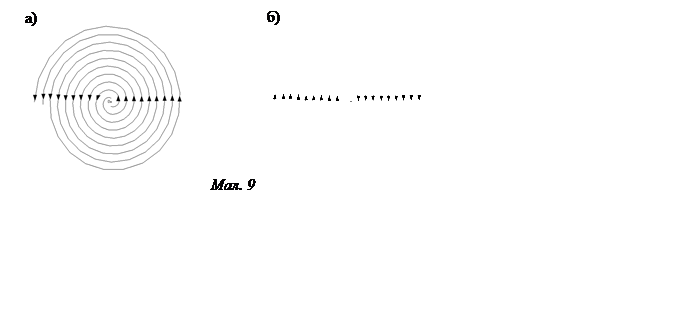
рух асимптотично стійкий. Точка, що зображена, у цьому випадку рухається по
спіралі, наближаючись до точки ![]() рівноваги , що у цьому
випадку називається стійким фокусом (мал. 9а).
рівноваги , що у цьому
випадку називається стійким фокусом (мал. 9а).
б) Якщо ![]() , то
, то ![]() при
при ![]() . Точка,
що зображена, віддаляється від точки
. Точка,
що зображена, віддаляється від точки ![]() спіралі, що аналогічна
розглянутої в попередньому випадку (мал. 9б). Точка спокою в цьому випадку
називається нестійким фокусом.
спіралі, що аналогічна
розглянутої в попередньому випадку (мал. 9б). Точка спокою в цьому випадку
називається нестійким фокусом.
 в)
Якщо
в)
Якщо ![]() , то рівняння (3.33) можна перетворити до
виду параметричних рівнянь еліпса
, то рівняння (3.33) можна перетворити до
виду параметричних рівнянь еліпса ![]() ,
, ![]() . Кожна точка, що
. Кожна точка, що ![]() зображує,
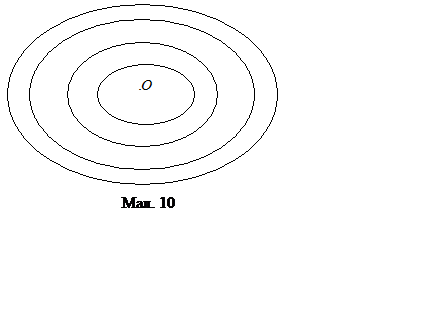
залежно від початкових збурень буде незліченну множину разів пробігати «свій»
еліпс, не прагнучи не віддалятися, не наближатися до центра. Точка спокою в
цьому випадку стійка по Ляпунову (але не асимптотична), є геометричним місцем
всіх еліпсів і називається центром. (мал. 10).
зображує,
залежно від початкових збурень буде незліченну множину разів пробігати «свій»
еліпс, не прагнучи не віддалятися, не наближатися до центра. Точка спокою в
цьому випадку стійка по Ляпунову (але не асимптотична), є геометричним місцем
всіх еліпсів і називається центром. (мал. 10).
3) Корені характеристичного рівняння дійсні й рівні ![]() .
.
Загальне розв'язання (3.32) має вигляд
![]() , в
, в![]() ,
,
де постійні зв'язані між собою лінійними рівняннями.
а) Якщо ![]() , то при
, то при ![]()
![]() швидше, ніж
швидше, ніж ![]() прагне
до нескінченності, тому
прагне
до нескінченності, тому ![]() при
при ![]() . Отже, точка спокою асимптотично стійка й
називається, як й у п. 1.а), стійким вузлом.
. Отже, точка спокою асимптотично стійка й
називається, як й у п. 1.а), стійким вузлом.
б) Якщо ![]() , то
, то ![]() при
при ![]() . Стан спокою нестійкий, точка спокою
називається нестійким вузлом.
. Стан спокою нестійкий, точка спокою
називається нестійким вузлом.
II. Одне з характеристичних чисел дорівнює нулю, наприклад, ![]() ,
, ![]() . Тоді загальне
розв'язання системи має вигляд
. Тоді загальне
розв'язання системи має вигляд
![]() ,
,![]() .
.
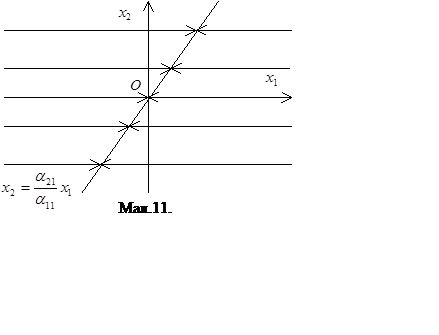
а) Якщо ![]() , те
, те ![]() при
при ![]() . Тоді на кожній траєкторії точки, що зображують,
наближаються до лежачій на цій траєкторії точці
. Тоді на кожній траєкторії точки, що зображують,
наближаються до лежачій на цій траєкторії точці ![]() с покою
с покою ![]() , (
, (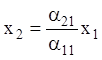 або)
(мал.11).
або)
(мал.11).
Таким чином, всі точки прямій 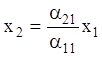 , у
тому числі й точка спокою
, у
тому числі й точка спокою ![]() є стійкою по Ляпунову
(але не асимптотично).
є стійкою по Ляпунову
(але не асимптотично).
б) Якщо ![]() , то точка спокою нестійка.
, то точка спокою нестійка.
III. Обидва характеристичних числа дорівнюють нулю ![]() . Тоді загальне розв'язання системи має
вигляд
. Тоді загальне розв'язання системи має
вигляд
![]() ,
, ![]() .
.
При цьому можливі такі варіанти
а) ![]()
![]()
![]() ,
,
![]() . Точка спокою стійка неасимптотично.
. Точка спокою стійка неасимптотично.
б) ![]() . У цьому випадку точка спокою, очевидно,
нестійка.
. У цьому випадку точка спокою, очевидно,
нестійка.
Зауваження 1. Рівняння фазових траєкторій можна відразу одержувати не в параметричної, а у звичайній формі. Розділивши друге рівняння (3.28) на перше, знайдемо диференціальне рівняння фазових траєкторій у вигляді
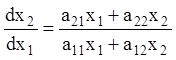 ,
(3.34)
,
(3.34)
інтегруючи яке одержимо
інтегральні криві, що збігаються з фазовими траєкторіями руху ![]() системи(3.28). При цьому точка спокою
системи
системи(3.28). При цьому точка спокою
системи ![]() ,
, ![]() є
особливою точкою рівняння (3.34). Таким чином, класифікація точок спокою тісно
пов'язана із класифікацією особливих точок.
є
особливою точкою рівняння (3.34). Таким чином, класифікація точок спокою тісно
пов'язана із класифікацією особливих точок.
Зауваження 2. Відповідно до теорем Ляпунова питання про стійкість і нестійкість автономної лінійної системи визначається видом коренів характеристичного рівняння й для систем невисокого порядку особливого труда не становить. Але зі зростанням порядку трудомісткість розв'язання зростає багаторазово. У цих випадках істотного значення набувають різні непрямі ознаки (критерії) стійкості, за допомогою яких можна зробити висновок про характер коренів, і, отже, про стійкість системи, не вирішуючи відповідного рівняння.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.