Багато проблем техніки й, особливо, математичної фізики (коливання струни й мембрани, теплопередача, дифузія й т.д.) приводяться до інтегрування диференціальних рівнянь у частинних похідних. Нагадаємо, що диференціальним рівнянням у частинних похідних називають рівняння, що містять одну або кілька функцій, що залежать від двох або більше аргументів, самі аргументи, а також частинні похідні по цим аргументах. Порядок старшої частинної похідної називають порядком рівняння в частинних похідних.
Далі коротко розглянемо тільки рівняння в частинних похідних 1-го порядку й у першу чергу ті, розв'язання які тісно пов'язані з розв'язанням систем звичайних диференціальних рівнянь.
Рівняння в частинних похідних першого порядку з однією невідомою функцією має вигляд
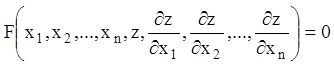 . (4.1)
. (4.1)
У випадку двох незалежних змінних рівняння (4.1) записують:
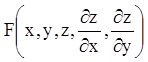 (4.2)
(4.2)
або, користуючись
позначеннями Монжа, 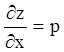 ,
, 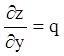
![]() .
(4.3)
.
(4.3)
У рівняння (4.1) або (4.2) може явно не входити шукана функція або незалежні змінні, але обов'язково повинна входити хоча б одна частинна похідна.
Проінтегрувати будь-яке диференціальне рівняння в частинних похідних –
значить знайти всі розв'язання даного рівняння. Природно очікувати, що
розв'язань буде нескінченна множина, виходячи хоча б з таких розумінь: звичайні
диференціальні рівняння можна формально розглядати як окремий випадок рівняння
в частинних похідних, коли число незалежних змінних ![]() ; але
всяке звичайне диференціальне рівняння має нескінченну множину розв'язань
(відповідних різним значенням довільних постійних); ми й поготів вправі очікувати
нескінченного числа розв'язань від рівняння, що містить більше одного
незалежного змінного. Попередні зазначення на характер довільних елементів, що
входять у розв'язання рівнянь у частинних похідних, ми можемо одержати з
окремих випадків, де легко знайти загальне розв'язання. Наприклад, розглянемо
рівняння
; але
всяке звичайне диференціальне рівняння має нескінченну множину розв'язань
(відповідних різним значенням довільних постійних); ми й поготів вправі очікувати
нескінченного числа розв'язань від рівняння, що містить більше одного
незалежного змінного. Попередні зазначення на характер довільних елементів, що
входять у розв'язання рівнянь у частинних похідних, ми можемо одержати з
окремих випадків, де легко знайти загальне розв'язання. Наприклад, розглянемо
рівняння
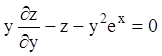 . (4.4)
. (4.4)
Воно містить тільки частинну похідну по ![]() , при
обчисленні якої
, при
обчисленні якої ![]() вважається постійною
(фіксується). Якщо ж
вважається постійною
(фіксується). Якщо ж ![]() вважати постійною величиною, то
рівняння (4.4) можна розглядати як звичайне рівняння із шуканою функцією
вважати постійною величиною, то
рівняння (4.4) можна розглядати як звичайне рівняння із шуканою функцією ![]() й незалежної змінної
й незалежної змінної ![]() . Але очевидно, що зміна
. Але очевидно, що зміна ![]() викликає зміну цього звичайного
диференціального рівняння, і тому
викликає зміну цього звичайного
диференціального рівняння, і тому ![]() потрібно розглядати як
його параметр. Тоді звичайне диференціальне рівняння запишеться
потрібно розглядати як
його параметр. Тоді звичайне диференціальне рівняння запишеться 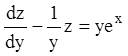 – це лінійне диференціальне рівняння
першого порядку з параметром
– це лінійне диференціальне рівняння
першого порядку з параметром ![]() і його розв'язання
і його розв'язання
![]() ,
(4.5)
,
(4.5)
для того щоб (4.5) було
розв'язанням рівняння (4.4), необхідно й досить, щоб ![]() -
було довільною функцією. Тоді загальне розв'язання рівняння (4.4) має вигляд
-
було довільною функцією. Тоді загальне розв'язання рівняння (4.4) має вигляд ![]() .
.
Як бачимо, загальне розв'язання рівняння в частинних похідних 1-го порядку, на відміну від звичайного диференціального рівняння, містить не довільну постійну, а довільну функцію.
Для рівняння 1-го порядку (4.1), припускаючи його дозволеним щодо
однієї із частинних похідних, наприклад ![]() :
:
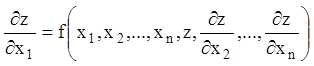 , (4.6)
, (4.6)
Задачу Коші формулюють так: знайти розв'язання
![]() рівняння (4.6) , що при заданому значенні
рівняння (4.6) , що при заданому значенні ![]() звертається в задану функцію інших
незалежних змінних при
звертається в задану функцію інших
незалежних змінних при
![]() ,
, ![]() .
(4.7)
.
(4.7)
Існування такого розв'язання ми доведемо тим, що дамо метод його побудови за допомогою інтегрування систем звичайних диференціальних рівнянь.
У випадку двох незалежних змінних (4.2) задача інтегрування рівняння із частинними похідними, а також задача Коші допускають просту геометричну інтерпретацію. Розглянемо рівняння (4.2) дозволене щодо однієї частинної похідної
![]() .
(4.8)
.
(4.8)
Знайти розв'язання рівнянь (4.2), (4.8) це, виходить, знайти функцію
![]() .
(4.9)
.
(4.9)
яка в координатному просторі ![]() зображує деяку поверхню, що називають інтегральною
поверхнею рівняння (4.8). Таким чином, задача знаходження розв'язання
рівнянь у частинних похідних є задачею знаходження інтегральних поверхонь. Якщо
розглядати рівняння (4.9) як визначальну поверхню, то дотична площина до неї в
точці
зображує деяку поверхню, що називають інтегральною
поверхнею рівняння (4.8). Таким чином, задача знаходження розв'язання
рівнянь у частинних похідних є задачею знаходження інтегральних поверхонь. Якщо
розглядати рівняння (4.9) як визначальну поверхню, то дотична площина до неї в
точці ![]() виражається рівнянням
виражається рівнянням
![]() ,
(4.10)
,
(4.10)
де![]() поточні
координати,
поточні
координати, ![]() і
і ![]() кутові
коефіцієнти дотичної площини. Таким чином, рівняння в частинних похідних (4.3)
виражає співвідношення між координатами
кутові
коефіцієнти дотичної площини. Таким чином, рівняння в частинних похідних (4.3)
виражає співвідношення між координатами ![]() точки
шуканої інтегральної поверхні й кутових коефіцієнтів
точки
шуканої інтегральної поверхні й кутових коефіцієнтів![]() і
і ![]() дотичною площини до цієї поверхні в цій
точці. Задача Коші для рівняння (4.8) з початковими умовами
дотичною площини до цієї поверхні в цій
точці. Задача Коші для рівняння (4.8) з початковими умовами
![]() ,
, ![]() .
(4.11)
.
(4.11)
інтерпретується так: знайти інтегральну поверхню, що проходить через просторову криву (4.11).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.