Диференціальні рівняння в частинних похідних першого порядку, страница 3

Має місце й зворотне твердження: якщо є кожним з розв'язань рівняння (4.17), те  є першим інтегралом системи (4.18).

Дійсно, підставимо в  замість  будь-яке розв'язання системи (4.18) і обчислимо повний диференціал цієї функції

.

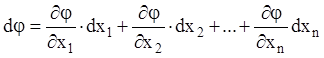Оскільки в  підставлене розв'язання системи (4.18) маємо право, з огляду на рівності (4.18), замінити  на  ( – коефіцієнт пропорційності), і вираз запишеться

.

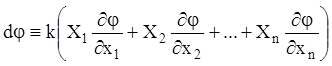Але , по припущенню, задовольняє рівнянню (4.17), значить . Як відомо, форма першого диференціала не змінюється при переході до іншим змінних, або, як говорять, є інваріантною. Підставивши в  розв'язання системи (4.18), ми одержали функцію однієї змінної в цьому випадку  й, як опинилося, її диференціал дорівнює нулю. Інакше кажучи, одержали функцію, похідна якої по  (після підстановки) є тотожним нулем, тобто  не залежить від  й є постійною. А це означає, що  є перший інтеграл системи (4.18).

Таким чином, ми встановили еквівалентність поняття інтеграла системи (4.18) і розв'язання рівняння в частинних похідних (4.17).

Раніше були доведено , що якщо

, ,…,...

є першими незалежними інтегралами системи (4.18), то будь-яка диференційована функція цих інтегралів  теж буде інтегралом цієї системи. А це означає, що довільна функція від будь-яких розв'язань рівняння (4.17) теж є розв'язанням цього рівняння. Більш того, має місце наступне твердження:

Якщо , ,…,є першими незалежними інтегралами системи (4.18), то функція

,                                                (4.20)

де  - довільна диференційована функція, є загальним розв'язанням рівняння (4.19) , тобто містить будь-яке частинне розв'язання цього рівняння.

Доведення.

Нехай  - перші незалежні інтеграли системи (4.18). Додаючи до них який завгодно новий інтеграл цієї ж самої системи, наприклад  (4.20), будемо мати

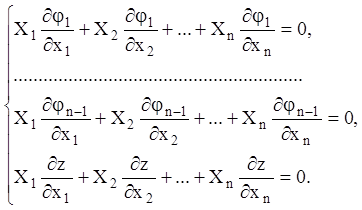                             (4.21)

Система (4.21) є лінійною однорідною алгебраїчною системою для визначення  функцій  і має ненульове розв'язання (ми думаємо, що хоча б один з ) тоді й тільки тоді, коли визначник цієї системи тотожно дорівнює нулю, тобто

.                                          (4.22)

Звідси, у силу основної теореми про якобіан, маємо, що між функціями  й  існує функціональна залежність

                                                (4.23)

(тотожна відносно ). Відзначимо, що у функціональному визначнику, що стоїть в лівій частині рівності (4.22), свідомо один з мінорів  порядку останнього рядка не дорівнює тотожно нулю. Справді, якщо система (4.18) має неособливі початкові значення , причому , то в припущенні, що в системі (4.18)  узяте за незалежну змінну й перші інтеграли мають вигляд  при значенні змінних, близьких до початкових

.

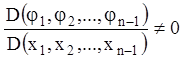А це означає, що в силу тієї ж теореми про якобіан, співвідношення (4.23) можна розв'язати щодо функції , тобто одержуємо

.                                                 (4.24)

Виходить, будь-яке розв'язання рівняння (4.17) міститься у формулі (4.24). Теорема доведена й формула (4.24) дає загальне розв'язання рівняння (4.17)

Висновок: для того щоб знайти загальне розв'язання лінійного однорідного рівняння в частинних похідних (4.17), необхідно побудувати еквівалентну йому систему звичайних диференціальних рівнянь (4.18) і знайти  незалежних інтегралів цієї системи. Тоді , де  - довільна диференційована функція, і буде загальним розв'язанням рівняння (4.17).

Повертаючись до рівняння (4.13), можемо сформулювати алгоритм його інтегрування (розв'язання рівняння (4.13) зводиться до розв'язання рівняння (4.16)):

1)  складаємо систему

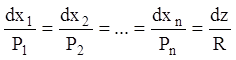                                             (4.25)

еквівалентну рівнянню

,

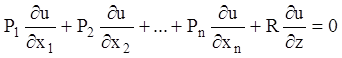і, розв’язав її, знаходимо  перших незалежних інтегралів

2)  дорівнюємо до нуля або до постійного довільну диференційовану функцію від цих інтегралів, тобто

.                                              (4.26)