Диференціальні рівняння в частинних похідних першого порядку, страница 5

.                                                        (4.32)

Тоді, крім із (4.31) і (4.32) параметри  й , одержуємо рівняння інтегральної поверхні

 або

 – диференційована функція.

Задача Коші. Вона ставиться так: визначити інтегральну поверхню, що проходить через дану криву . Попередні міркування показують, що задача має єдине розв'язання, якщо тільки крива не є характеристикою. Геометричне розв'язання задачі наступне: необхідно взяти сукупність характеристик, які проходять через точки заданої кривої , вони й утворять шукану поверхню.

Якщо  задано параметрично

то, підставляючи цей вираз в (4.31), одержимо вираз  і  як функції від ; крім , знаходимо шукане співвідношення між  й . Ще раз підкреслимо, що характеристики - такі криві, для яких задача Коші не визначена.

Приклад 2. Знайти поверхню, що задовольняє рівнянню

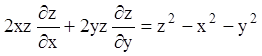
і проходить через криву (окружність)

, 

Розв’язання. Записуємо еквівалентну систему

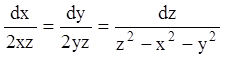
і знаходимо її перші інтеграли. З рівняння

.

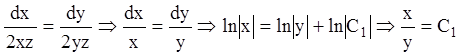Далі

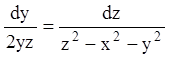 т. к. , те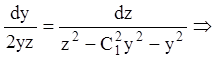

.

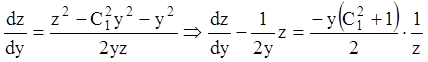Це рівняння Бернуллі, розв’язав яке, одержуємо його інтеграл

 або .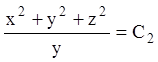

Тоді загальний інтеграл вихідного рівняння запишеться

.

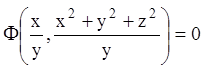Виключимо тепер з рівнянь

,  ,  ,  .

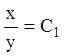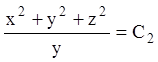Із другого й четвертого рівнянь маємо 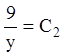, звідки 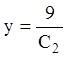. Тоді з першого рівняння 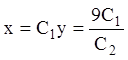, тобто 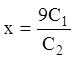. Із третього рівняння одержуємо 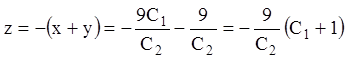. Тепер можемо знайти залежність між  й , використовуючи друге рівняння

.

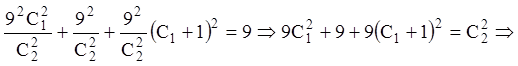
Заміняючи тепер  відповідними їм вираженнями, одержуємо рівняння шуканої поверхні

.

4.4. Нелінійні рівняння в частинних похідних першого порядку.

4.4.1. Утворення диференціального рівняння в частинних похідних. Повний, загальний й особий інтеграли.

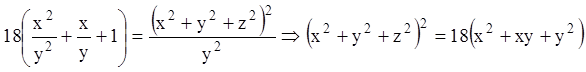Переходячи до інтегрування рівнянь у частинних похідних першого порядку довільного виду, зупинимося спочатку на утворенні самого диференціального рівняння й уведемо деякі нові поняття.

Нехай дане співвідношення

,                                                      (4.33)

яке визначає  як неявну функцію  й , і містить дві довільні незалежні постійні  й . Диференціюючи (4.33) по  й одержимо

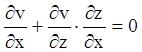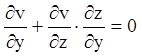,  .                                      (4.34)

Крім  і  з (4.33) і (4.34), одержуємо

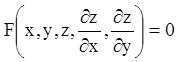.                                                 (4.35)

Співвідношення (4.33) називають повним інтегралом рівняння (4.35). Це поняття вперше ввів Лагранж. Отриманий результат узагальнюється на випадок довільного числа незалежних змінних, а тому можна дати таке визначення повного інтеграла.

Означення. Повним інтегралом диференціального рівняння першого порядку в частинних похідних називають таке співвідношення між змінними, котре задовольняє даному рівнянню й містить стільки довільних постійних, скільки в рівнянні незалежних змінних.

Покладемо тепер, що  й  не довільні постійні, а є функціями від  й . Спробуємо підібрати ці функції так, щоб виключення їх з (4.33), (4.34) дало те ж саме рівняння (4.35). Очевидно, для цього необхідно, щоб похідні, обчислені у випадку, якщо  й  залежать від  й  , мали ту ж саму форму, що й при постійних  й . Оскільки при змінних  й

,

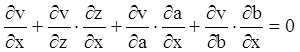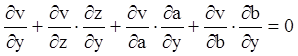,                                       (4.36)

т, з огляду на рівності (4.34), повинні виконуватися рівності

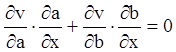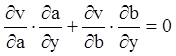,  .                                (4.37)

Останні рівності можна одержати, поклавши , .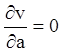

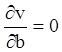Якщо рівняння , , 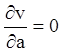 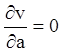спільні, то вони визначають три функції , ,  змінних  й . Визначений таким способом інтеграл  зовсім не містить довільних параметрів і називається особим інтегралом. Якщо ж  і  не рівні одночасно нулю, то з рівнянь (4.37) треба, що визначник системи

.

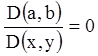Якщо всі елементи цього визначника нулі, то =const, =const і ми маємо знову повний інтеграл. Якщо ж не всі елементи визначника нулі, то між  й  існує співвідношення, не залежне від   й . Задамо його рівністю

.

Тоді рівності (4.37) представляться у вигляді

,   ,

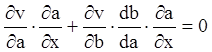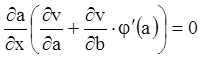або

,  

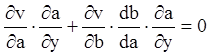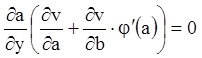
Оскільки по припущенню  не постійна, те отримані рівності виконуються, якщо

.

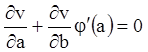З нього знаходимо , а потім й .

Три рівняння

, ,

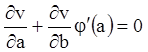
дають інтеграл рівняння (4.35), залежний від довільної функції . Його називають загальним інтегралом рівняння (4.35).

Геометричний зміст повного інтеграла – сімейство поверхонь, що залежать від двох (у загальному випадку від декількох) параметрів  й , а особливого – огинаюча сімейства поверхонь повного інтеграла. Установлюючи довільне співвідношення , одержуємо сімейство поверхонь, що залежать тільки від одного параметра . Якщо тепер виключити параметр  із рівнянь