Диференціальні рівняння в частинних похідних першого порядку, страница 4

Неявна функція  від  змінних  визначається рівністю (4.26) і являє собою інтеграл рівняння (4.13). Але твердження, що співвідношення (4.26) є й загальним інтегралом рівняння (4.13), тобто містить всі частинні інтеграли рівняння (4.13), мають потребу в додаткових дослідженнях. Для того щоб рівняння (4.16) було лінійним однорідним із шуканою функцією від  незалежних змінних, необхідно розглядати в ньому поруч із незалежними змінними  теж  як незалежну змінну. А цим самим на  накладаються по суті, додаткові вимоги: перетворити (4.16) у тотожність не відносно , а відносно й . Це дослідження проведене й виявляється, що всі інтеграли рівняння (4.13), за винятком особливих, не залежних ні від однієї довільної постійної, задовольняють рівності (4.26), тобто останнє і є загальним інтегралом рівняння (4.13).

Приклад 1. Розв’язати рівняння .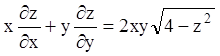

Розв’язання. Записуємо відповідну систему звичайних рівнянь

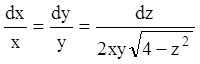
з рівняння 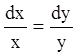 знаходимо  з рівняння 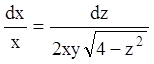, з огляду на те що , знаходим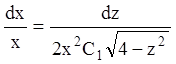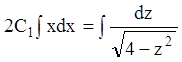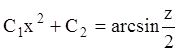о ; ; , або .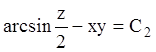

Тому загальний інтеграл буде

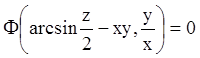
або

.

4.3 Лінійне рівняння з двома незалежними змінними. Геометричне тлумачення

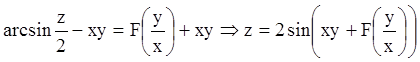Відомо, що звичайне диференціальне рівняння першого порядку, дозволене відносно похідній  визначає на площині поле напрямків. Вище встановлене, що рівняння в частинних похідних (4.2), (4.3) установлює співвідношення між координатами  точки шуканої інтегральної поверхні й кутових коефіцієнтів  і  дотичною площини до цієї поверхні в цій точці.

Розглянемо лінійне рівняння першого порядку

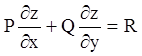 або ,                               (4.27)

де функції від . Кожне розв'язання цього рівняння  визначає деяку поверхню, так називану інтегральну поверхню . Дотична площина до поверхні  в точці  має вигляд (4.10), а нормаль до поверхні

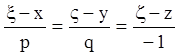.                                               (4.28)

Звідси робимо висновок, що пряма, представлена рівнянням

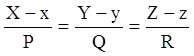,                                                 (4.29)

яка, внаслідок рівняння (4.27), перпендикулярна нормалі (4.28) (тому що ), буде лежати в дотичної площини (4.10). Кожній точці  простору відповідає певна пряма (4.29), що проходить через  й яку будемо називати прямої точки  (випадок і не існування прямій (4.29) не розглядається). Тоді задачу інтегрування рівняння (4.27) можна сформулювати так: знайти таку поверхню , щоб дотична площина в кожній її точці проходила через пряму (4.29) (містила цю пряму), що відповідає цій точці.

Якщо відомі всі поверхні, які мають цю властивість, то буде відомим і загальним інтегралом рівняння (4.27). Функції  визначають той закон, по якому змінюється напрямок прямій (4.29), коли переміщається точка . Така геометрична постановка задачі інтегрування рівняння (4.27) приводить нас до відшукання ліній, які в кожній своїй точці стосуються відповідній прямій (4.29), тобто в кожній точці дотичної до лінії  є пряма (4.29) цієї точки. Дійсно, якщо деяка поверхня є геометричним місцем ліній , тобто утворена лініями , то в кожній точці цієї поверхні дотична (пряма (4.29)) до лінії , що проходить через цю точку, буде лежати в дотичної площини до поверхні. Виходить, поверхня є інтегральною поверхнею, і її рівняння буде задовольняти рівнянню (4.27). Легко бачити, що й навпаки, будь-яка інтегральна поверхня, тобто рівняння якої задовольняє рівнянню (4.27), може бути покрита лініями , тобто є геометричним місцем ліній .

Дійсно, якщо поверхня  задовольняє рівнянню (4.27), то в кожній її точці  відповідна пряма (4.29) лежить у дотичної площини. Виходить, можна шукати такі криві, які лежать на цій поверхні і які в кожній своїй точці торкалися б відповідній прямій (4.29).

Установимо рівняння кривих . Відомо, що напрямні косинуси дотичної пропорційні величинам ; при збігу двох напрямків величини, пропорційні їхнім напрямним косинусам, повинні бути пропорційні між собою. Виходить, для знаходження кривих  маємо систему:

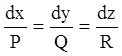.                                                          (4.30)

Її загальний інтеграл

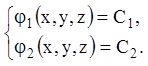.                                                        (4.31)

Інтегральні криві, обумовлені системою (4.30) називають характеристиками рівняння (4.27). Виходить, будь-який інтеграл рівняння (4.27) є геометричним місцем характеристик і відшукання цих інтегралів зводиться до знаходження характеристик. Через кожну точку простору проходить одна й тільки одна характеристика, що торкається відповідній прямій (4.29). Якби ми проінтегрували (4.30) і одержали (4.31), то, щоб одержати поверхню, утворену цими кривими, необхідно встановити між  і  довільне співвідношення, наприклад,