Чисельник останнього виразу буде рівнятися нулю, якщо (4.41)
виконується тотожно. Виходить, права частина рівності (4.43) не залежить від ![]() й являє собою звичайне диференціальне
рівняння першого порядку із шуканою функцією
й являє собою звичайне диференціальне
рівняння першого порядку із шуканою функцією ![]() .
Інтегруючи (4.43), знаходимо
.
Інтегруючи (4.43), знаходимо ![]() , виражену через
, виражену через ![]() і довільну постійну. Підстановка
останнього виразу в (4.42) і дає розв'язання системи (4.39), що містить одну
довільну постійну. Виходить, необхідною й достатньою умовою повної
інтегрируємості системи (4.39) є тотожне виконання співвідношення (4.41). Коли
це має місце, інтегрування системи (4.39) приводиться до інтегрування двох
звичайних диференціальних рівнянь першого порядку. Співвідношення (4.41) часто
називають умовою спільності системи (4.39).
і довільну постійну. Підстановка
останнього виразу в (4.42) і дає розв'язання системи (4.39), що містить одну
довільну постійну. Виходить, необхідною й достатньою умовою повної
інтегрируємості системи (4.39) є тотожне виконання співвідношення (4.41). Коли
це має місце, інтегрування системи (4.39) приводиться до інтегрування двох
звичайних диференціальних рівнянь першого порядку. Співвідношення (4.41) часто
називають умовою спільності системи (4.39).
Задача інтегрування рівняння
![]() , (4.45)
, (4.45)
де![]() –
задані функції, по суті зводиться до попередній. Запишемо рівняння (4.45) у вигляді
(припускаємо, що
–
задані функції, по суті зводиться до попередній. Запишемо рівняння (4.45) у вигляді
(припускаємо, що ![]() ):
):
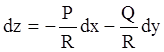 .
.
Тоді, позначивши
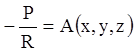 ,
, 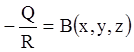
зведемо його до системи (4.39). Умова (4.41) повної інтегрованості
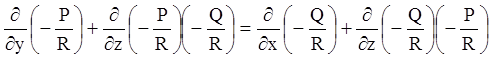
після виконання операцій диференціювання й спрощень приводиться до виду:
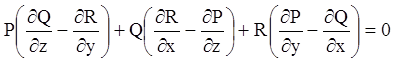 . (4.46)
. (4.46)
Умова (4.46) не змінюється при круговій перестановці ![]() й
й ![]() . Значить
ми одержали б цю же умову й тоді, якби замість
. Значить
ми одержали б цю же умову й тоді, якби замість ![]() невідомої
функції вибрали б
невідомої
функції вибрали б ![]() або
або ![]() .
.
Перейдемо тепер до викладу методу Лагранжа - Шарпи, що дає загальний прийом знаходження повного інтеграла рівняння
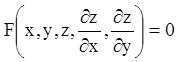 .
(4.47)
.
(4.47)
Ідея методу полягає в тому, що ми шукаємо друге рівняння
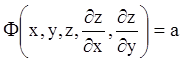 ,
(4.48)
,
(4.48)
де ![]() –
довільна постійна, за умови, щоб система цих двох рівнянь була повністю
інтегрувальною. Друге рівняння підбирається так, щоб воно містило довільну
постійну. Розв'язання, таким чином, буде містити дві довільні постійні, тобто
буде повним інтегралом.
–
довільна постійна, за умови, щоб система цих двох рівнянь була повністю
інтегрувальною. Друге рівняння підбирається так, щоб воно містило довільну
постійну. Розв'язання, таким чином, буде містити дві довільні постійні, тобто
буде повним інтегралом.
Покладемо, що ![]() підібрано так, що (4.47) і (4.48)
розв'язно відносно
підібрано так, що (4.47) і (4.48)
розв'язно відносно ![]() й
й ![]() і
систему
і
систему
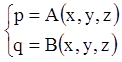 (4.49)
(4.49)
є повністю інтегрованою. Тоді умова повної інтегрованості запишеться
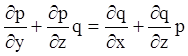 .
(4.50)
.
(4.50)
Тепер необхідно обчислити всі частинні похідні, що входять у тотожність
(4.50). Для цього будемо диференціювати (4.47) і (4.48) по ![]() , розглядаючи
, розглядаючи ![]() і
і ![]() як неявні функції
як неявні функції ![]() .
Одержимо
.
Одержимо
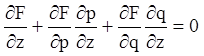 ,
,
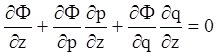 .
.
Звідки
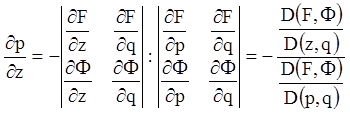 ;
;
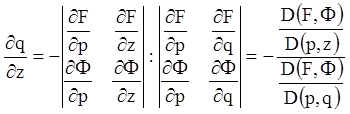 .
.
Аналогічно, диференціюючи по ![]() й
й ![]() , будемо мати
, будемо мати
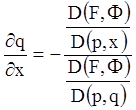 ;
; 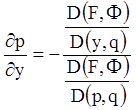
Якщо тепер вираз для ![]() ,
, ![]() ,
, ![]() ,
, ![]() внесемо в (4.50), то останнє буде мати
вигляд
внесемо в (4.50), то останнє буде мати
вигляд
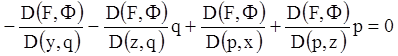 ,
,
або, якщо введемо позначення
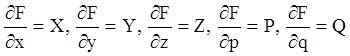
і розпишемо функціональні визначники
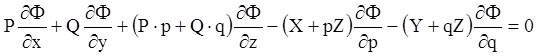 . (4.51)
. (4.51)
Виходить, допоміжна функція ![]() повинна задовольняти
лінійному рівнянню в частинних похідних з п'ятьма незалежними змінними.
Відповідному рівнянню (4.51) система звичайних диференціальних рівнянь буде
мати вигляд
повинна задовольняти
лінійному рівнянню в частинних похідних з п'ятьма незалежними змінними.
Відповідному рівнянню (4.51) система звичайних диференціальних рівнянь буде
мати вигляд
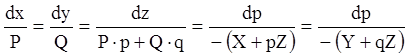 . (4.52)
. (4.52)
У нашому випадку немає необхідності знати загальний інтеграл системи
(4.52), досить знати який-небудь перший інтеграл цієї системи за умови, щоб
рівняння ![]() ,
, ![]() розв’язувалося
відносно
розв’язувалося
відносно ![]() й
й ![]() .
.
Висновок: щоб знайти
повний інтеграл рівняння (4.47) потрібно знайти спочатку такий перший інтеграл F=a системи (4.52), щоб
визначник 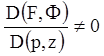 , і потім вирішити два рівняння
, і потім вирішити два рівняння ![]() ,
, ![]() відносно
відносно
![]() й
й ![]() .
Підставляючи знайдені вираження
.
Підставляючи знайдені вираження ![]() й
й ![]() у рівняння
у рівняння ![]() ,
одержимо повністю інтегроване рівняння в повних диференціалах. Загальний
інтеграл останнього буде містити другу довільну постійну
,
одержимо повністю інтегроване рівняння в повних диференціалах. Загальний
інтеграл останнього буде містити другу довільну постійну ![]() , а це й буде повний інтеграл рівняння
(4.47).
, а це й буде повний інтеграл рівняння
(4.47).
В окремих випадках інтегрування рівняння (4.47) залежно від його структури значно спрощується.
Приклад 1. Знайти повний інтеграл рівняння
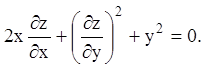
Розв’язання. У наших позначеннях
![]() ,
,
тоді
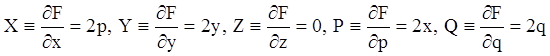 .
.
Тепер система (4.52) запишеться
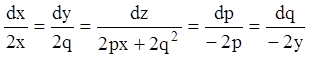 .
.
Звідси одержуємо інтегрувальну комбінацію
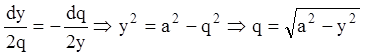 ,
,
де ![]() -
довільна постійна.
-
довільна постійна.
З огляду на, що 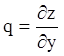 , після підстановки у
вихідне рівняння, одержуємо
, після підстановки у
вихідне рівняння, одержуємо
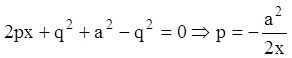
Підставляючи значення ![]() й
й ![]() у рівняння Пфаффа, будемо мати
у рівняння Пфаффа, будемо мати
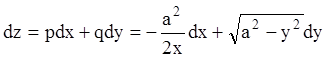 .
.
Тоді
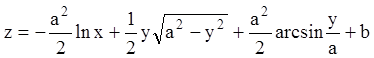
і є повним інтегралом системи.
Приклад 2. Знайти повний й особий інтеграли рівняння
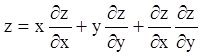 .
.
Розв’язання.
![]() . Значить
. Значить ![]() . Система
(4.52) запишеться
. Система
(4.52) запишеться
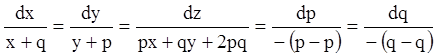 .
.
Виходить,
можемо взяти ![]() . Тоді
. Тоді
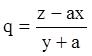
Рівняння Пфаффа запишеться
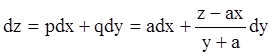
Інтегруючи, одержуємо, (![]() – параметр)
– параметр)
![]() ,
, ![]()
Далі
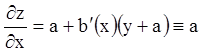 , тоді
, тоді ![]() ,
, ![]() .
.
Повний інтеграл рівняння запишеться
![]() , або
, або ![]()
Для знаходження особого інтеграла одержуємо 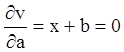 ,
, 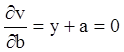 . Значить
. Значить ![]() .
Підставляючи в
.
Підставляючи в ![]() , одержуємо
, одержуємо ![]() , або
, або ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.