Диференціальні рівняння в частинних похідних першого порядку, страница 2

Зауваження. Та ж геометрична мова, що для рівнянь із двома незалежними змінними користується тривимірним простором, застосовується за аналогією до будь-якого числа змінних, причому використається поняття многомірного простору. Сукупність числових значень  називають точкою – мірного простору; розв'язання рівняння (4.1) виду

 -

є інтегральна поверхня  вимірів у цьому просторі. Початкові умови задачі Коші (4.7) представляють поверхню  вимірів, через яку повинна пройти шукана інтегральна поверхня.

Виходячи із задачі Коші, можемо затверджувати, що сукупність всіх частинних розв'язань рівняння в частинних похідних першого порядку вийде, якщо давати всілякі (припустимі) види тої функції  від  аргументів, що входить в умови Коші (4.7). У цьому значенні можна сказати, що сукупність розв'язань рівняння першого порядку залежить від однієї довільної функції – саме тієї, котра входить в умови Коші. Аналогічна сукупність частинних розв'язань рівняння -того порядку залежить від  довільних функцій  аргументів, що становлять умови Коші для рівняння -того порядку:

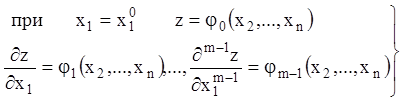                            (4.12)

Однак цим не вирішується питання про загальне розв'язання, тобто про таке вираження шуканого  у функції незалежних змінних, довільних постійних і функцій, з якого можна одержати будь-яке частинне розв'язання. У більшості випадків, крім рівнянь у частинних похідних першого порядку, представлення загального розв'язання, що як явно залежить від довільних функцій, неможливо.

4.2 Лінійні диференціальні рівняння в частинних похідних першого порядку

Лінійними рівняннями називають рівняння, які містять частинні похідні тільки в першому степені. Загальний вид лінійного рівняння в частинних похідних першого порядку такий:

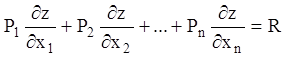                                         (4.13)

де - неперервні функції (разом зі своїми частинними похідними) незалежних змінних  й . Оскільки шукана функція  може входити в  и  в різних степенях, то рівняння типу (4.13) часто називають квазілінійним. Якщо , а  не залежать від , то таке рівняння називають лінійним однорідним рівнянням у частинних похідних. Виходить, воно буде мати вигляд

.

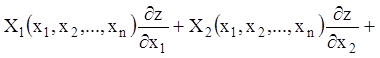
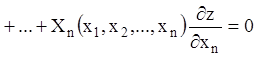Нехай

                                                     (4.14)

є інтегралом рівняння (4.13), тобто шукана функція визначається рівністю (4.14) як неявна функція від . Виходить, 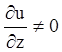 у деякій області зміни . Диференціюючи співвідношення (4.14), одержуємо

.

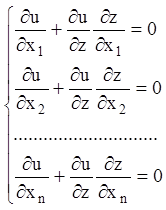Якщо тепер помножити перше із цих рівностей на , друге на , і т.д., останнє на  й скласти всі результати множення, одержимо

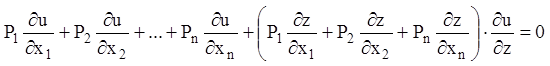
Вираження в круглих дужках тотожно дорівнює  (по припущенню  – розв'язання рівняння (4.13)), а тому остаточно одержуємо рівняння

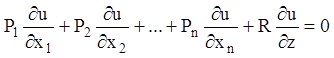                                    (4.16)

для знаходження функції  . Очевидно, що коефіцієнти рівняння (4.16) не містять шуканої функції  й вільний член рівняння дорівнює нулю, тобто рівняння (4.16) є лінійним однорідним рівнянням.

Висновок: знаходження розв'язань рівняння (4.13) зводиться до знаходження розв'язання лінійного однорідного рівняння (4.16).

У зв'язку із цим доцільно, насамперед, розглянути лінійне однорідне рівняння

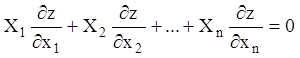,                                     (4.17)

де  шукана функція, а - функції тільки незалежних змінних  (і хоча б один з ).

Розв'язання рівняння (4.17) зводиться до розв'язання відповідної йому еквівалентної системи звичайних диференціальних рівнянь першого порядку.

Візьмемо систему звичайних диференціальних рівнянь у симетричній формі

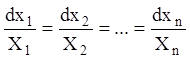,                                          (4.18)

яку називають відповідну рівнянню (4.17).

Нехай, наприклад,  - незалежна змінна, а  - функції, які є розв'язаннями системи (4.18). Відомо, що система (4.18) допускає  незалежних інтегралів

, ,…,...

Візьмемо кожного з них, наприклад, . Виходячи з визначення інтеграла, будемо мати

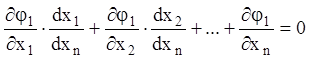
або

.

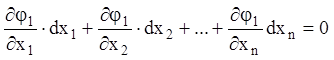Заміняючи в останнім рівнянні  пропорційними їм величинами  , одержуємо

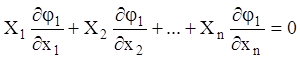.                                   (4.19)

Остання рівність є тотожністю, тому що воно має місце для будь-якої системи значень, які задовольняють системі (4.18), тобто незалежно від того, яке саме розв'язання цієї системи підставляти в  Виходить, функція  є розв'язанням рівняння (4.17)

Висновок: кожен інтеграл системи (4.18) є розв'язанням рівняння (4.17).