Теорія стійкості. Основні поняття. Дослідження на стійкість точок спокою

Розділ 3.

ТЕОРІЯ СТІЙКОСТІ

3.1 Основні поняття

Дослідження механічних, електричних й інших систем на стійкість є однієї з тих задач, правильне розв'язання яких відіграє першорядну роль при проектуванні цих систем. Математичною моделлю кожної таких систем є деяке диференціальне рівняння (або система таких рівнянь) разом з початковими або граничними умовами. Розв'язання цього диференціального рівняння (або цієї системи рівнянь) дає функціональну залежність параметрів, що характеризують стан системи від часу.

Властивість стійкості розв'язання диференціального рівняння – одне з умов так називаної коректності цього розв'язання. Під стійким тут розуміється таке розв'язання, що змінюється як завгодно мало при досить малих змінах початкових умов. Разом з тим при моделюванні реального процесу, що відбуває під впливом незліченної множини різних факторів, відкидаючи багато з них як несуттєві, одержуємо деяку ідеалізацію процесу у вигляді диференціального рівняння або системи рівнянь. Відповідність реального руху отриманому розв'язанню й навпаки буде спостерігатися в тих випадках, коли досліджувана система, її рух, або рівноважний стан є стійкими, а математична модель відображає всі основні особливості цієї системи. У противному випадку реальний рух може сильно відрізнятися від описуваного отриманим розв'язанням. Інтуїтивно під стійкими розуміють такі системи, які, виведені зовнішніми впливами, що збурюють, зі стану рівноваги, із часом знову повертаються до свого початкового (або як завгодно близькому до нього) стану.

Аналізуючи деякі найпростіші рухи з позицій інтуїтивного розуміння стійкості, можна затверджувати, що кулька на ввігнутій поверхні (у лунці) представляє стійку систему; кулька на опуклій поверхні – нестійку систему; кулька на горизонтальній поверхні буде перебувати в стані байдужої рівноваги (якщо її перекотити з одного положення в інше, то вона залишиться у своєму кінцевому положенні). Як більш складний приклад розглянемо систему автоматичного регулювання, тобто електромеханічний пристрій, що складається з об'єкта регулювання й регулятора. Роль регулятора полягає в тому, щоб підтримувати в регульованому об'єкті певний режим роботи. Говорять, що цей режим роботи є стійким, якщо при певнім настроюванні регулятора (початкові умови) у системі навіть при наявності деяких природних факторів, що збурюють, реалізується саме цей режим роботи.

Установленням критеріїв, по яких можна судити, чи буде розглянутий процес стійкий або нестійким, займається теорія стійкості руху або просто теорія стійкості. Вона є одним з основних розділів якісної теорії диференціальних рівнянь. Творцем теорії стійкості руху як математичної науки є А.М. Ляпунов (1857 – 1918). Досліджувані в цій теорії процеси описуються звичайними диференціальними рівняннями. Щодо розв'язань цих рівнянь введемо основні поняття теорії. Надалі, говорячи про стійкість розв'язання деякого диференціального рівняння (або системи рівнянь) будемо інтерпретувати як стійкість відповідного руху досліджуваного об'єкта, і навпаки, тобто будемо ототожнювати ці поняття.

Розв'язання   рівняння 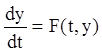 називається стійким по Ляпунову, якщо  , що для будь-якого іншого розв'язання  рівняння з початкової нерівності  маємо нерівність  при всіх .

Розв'язання  називається асимптотично стійким по Ляпунову, якщо воно стійко, і, крім того, існує таке , що будь-яке розв'язання  цього рівняння, для якого  має властивість .

Розв'язання  називається нестійким, якщо воно не є стійким.

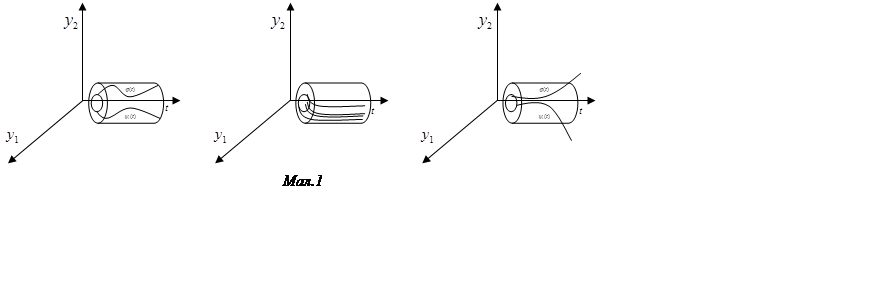
Дамо геометричне тлумачення уведених понять і визначень. Нехай  – інтегральна крива рівняння. Розв'язання : стійко, якщо будь-яка інша інтегральна крива  рівняння, що проходить при  через досить близьку до  точку, цілком міститься в як завгодно вузьку  – трубку, побудовану навколо кривій  (мал.1); асимптотично стійке, якщо будь-яка інтегральна крива  притягається до кривої  при  (мал.1); нестійке, якщо найдеться інтегральна крива  рівняння, що проходить при  через досить близьку до  точку, що попадає на границю як завгодно малої  – трубки, побудованої навколо кривій  (мал.1).

Таким чином, розв'язання  стійке по Ляпунову, якщо при близьких до нього по початкових умовах розв'язання залишаються близькими й для всіх  (див. мал. 1).

Приведемо приклади стійких і нестійких розв’язків.

Приклад 1. Дослідити на стійкість розв'язання диференціального рівняння 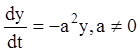, обумовлене початковою умовою ç .