Теорія стійкості. Основні поняття. Дослідження на стійкість точок спокою, страница 3

                                   (3.7)

то рух системи називається асимптотично стійким. Умови (3.7) геометрично варто розуміти так: при асимптотичної стійкості, що зображує точка  будь-якої фазової траєкторії повинна, ніде не виходити за межі сфери радіуса , необмежено наближатися до початку координат.

Це означає, що фізична система, рух якої розглядається, прагне повернутися у свій початковий рівноважний стан.

У випадку неасимптотичної стійкості точка, що  зображує, описує фазову траєкторію, що не прагне до початку координат, але цілком розташовану в межах сфери  радіуса . Це означає, що досліджувана фізична система, у цьому випадку не прагне повернутися у свій початковий рівноважний стан, але й не йде від нього далеко.

Означення стійкості можна сформулювати й трохи інакше, зберігши при цьому його сутність: незбурений рух (3.2) називається стійким по Ляпунову, якщо для  завжди  таке  що з умов

     

при всіх  будуть випливати нерівності

.

У противному випадку, рух називають нестійким (мал.5).

Фізичну систему називають стійкою, якщо стійкий при заданих умовах будь-який її незбурений рух (3.2).

Відзначимо, що визначення стійкості по Ляпунову відрізняється наступними особливостями:

а) передбачається, що малим збурюванням піддаються лише початкові умови. Це означає, що розглянута динамічна система є під впливом лише миттєво діючих збурювань, а збурений її рух відбувається при тих же силах, що й незбурений;

б) стійкість руху розглядається на нескінченно великому проміжку часу.

Реальні динамічні системи часто є під впливом постійно діючих сил, що збурюють, а процеси, що відбуваються в цих системах, звичайно, тривають протягом кінцевого відрізка часу. Дослідження стійкості руху системи в цих практично важливих випадках, як правило, може бути зведене до дослідження стійкості по Ляпунову.

3.3 Рівняння збуреного руху

З (3.6) маємо      Тому що функції  є розв’язанням системи (9.1), то, внесемо їх у цю систему, одержимо тотожності

 

Припускаючи, що функції  задовольняють умовам розкладності в ряд Тейлора, і, зробивши їхнє розкладання в зазначений ряд, одержимо

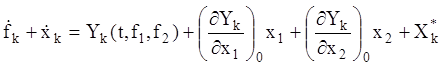
                      (3.8)

де  – сукупність членів, що містять  й  у степені вище першої.

Тому що  теж є розв’язаннями системи (3.1), тобто   те рівності (3.8) запишуться

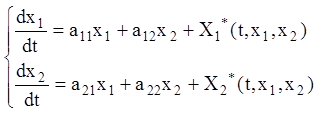,                                    (3.9)

де 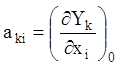 – функції часу  (в окремому випадку постійні).

Система (3.9) називається системою рівнянь збуреного руху. Позначивши через  всі члени правих частин рівнянь (3.9), перепишемо рівняння збуреного руху у вигляді

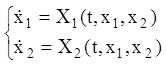.                                              (3.10)

Зокрема, якщо праві частини системи (3.10) не залежать від , тобто

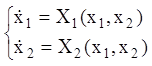 ,                                                (3.11)

то систему (3.11) називають автономною (стаціонарної), а її рух – сталим. Тоді систему (3.10) називають неавтономною (нестаціонарної), а її рух – несталим. Далі будемо розглядати автономні системи.

З (3.9) маємо, що при  праві частини систем (3.9) і (3.10) звертаються в нулі, тобто у випадку неавтономної системи  а у випадку автономної –  Із цього витікає, що функції

,                                               (3.12)

є розв’язанням системи рівнянь збуреного руху.

У попередньому пункті було показано, що не збуреному руху (3.2) системи (3.1) відповідають нульові значення всіх варіацій , тобто нульове (тривіальне) розв’язання (3.12) рівнянь збуреного руху. Із цього маємо, що дослідження на стійкість не збуреного руху (3.2) рівносильне дослідженню на стійкість нульового розв’язання (3.12) рівнянь збуреного руху.

У випадку якщо динамічна система описується лінійною однорідною системою диференціальних рівнянь

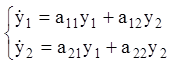,                                                (3.13)

то, підставивши в ці рівняння функції

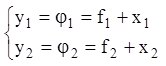,                                                (3.14)

де – збурені і незбурені рухи, а  – варіації, і з огляду на, що  є розв’язаннями системи (3.13), одержимо рівняння збуреного руху:

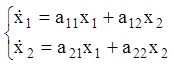                                                 (3.15)

Зрівнявши системи (3.13) і (3.15), робимо висновок, що лінійна однорідна система диференціальних рівнянь одночасно є й системою рівнянь збуреного руху.

Висновок: досліджуючи на стійкість нульове розв’язання системи (3.13), ми тим самим досліджуємо на стійкість будь-яке частинне розв’язання цієї системи. У цьому складається важлива характеристична властивість лінійних систем.