Теорія стійкості. Основні поняття. Дослідження на стійкість точок спокою, страница 2

Розв’язання. Інтегруючи, знаходимо загальне розв'язання . Використовуючи початкові умови, одержуємо . Як інше розв'язання візьмемо . Тоді для кожного  з початкової нерівності  в нашому випадку  повинна бути оцінка  вже для кожного . Ця оцінка, мабуть, має місце, якщо тільки . Значить розв'язання рівняння стійке. Більш того, тому що , то досліджуваний рух буде ще й асимптотично стійким.

Приклад 2. Дослідити на стійкість розв'язання рівняння 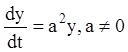, обумовлене умовою ç .

Розв’язання. Інтегруючи, одержуємо . Тоді  , що з початкової нерівності

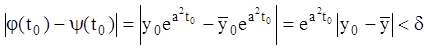
маємо 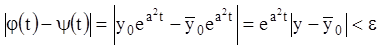 для . Але це неможливо, тому що  при . Тому досліджуваний рух нестійкий.

3.2 Дослідження на стійкість точок спокою

Будемо припускати, що розглянута динамічна система визначається двома змінними  й , якими залежно від характеру системи можуть бути просторові координати, швидкості, температури, струми й т.п. Будемо вважати, що система визначається тільки двома параметрами, маючи на увазі лише більшу наочність одержуваних результатів – всі ці результати, з відповідними змінами, будуть узагальнюватися для системи обумовленої   змінними.

Нехай рух системи описується нормальною системою диференціальних рівнянь виду

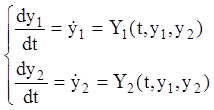,                                                        (3.1)

де t – час, ,  – задані функції змінних , задовольняючі теоремі існування й одиничності розв'язання нормальної системи.

Нехай, рух розглянутої динамічної системи визначається частинним розв'язанням

,                                                            (3.2)

нормальної системи (3.1), що задовольняє початковим умовам:

, ,                                       (3.3)

де  – задані числа. Розв'язання (3.2) і рух системи, що воно описує, називають незбуреним рухом.

Змінимо тепер умови (3.3), додавши початковим значенням  і  змінних  і  відповідно невеликі по модулі прирости  й , які називають збуреннями. Частинне розв’язання системи (3.1), що задовольняє зміненим початковим умовам

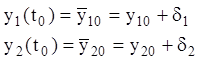,                                                  (3.4)

позначимо через

, .                                                  (3.5)

Розв’язання (3.5) і рух системи, їй обумовлене, називають збуреним рухом.

Введемо в розгляд різниці

                                            (3.6)

між значеннями змінних  в збуреному й незбуреному рухах і назвемо їхніми варіаціями величини . Якщо всі варіації дорівнюють нулю , то збурений рух (3.5) буде збігатися з незбуреним рухом (3.2). Таким чином, незбуреному руху відповідають нульові значення всіх варіацій .

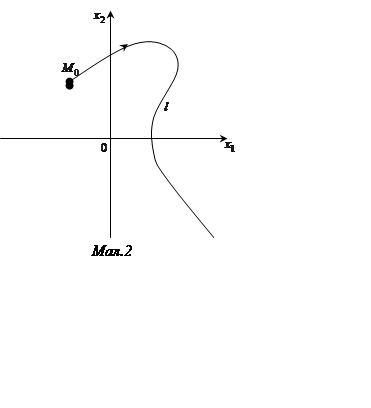
Візьмемо площину змінних , називаною фазовою площиною, і віднесемо її до декартової прямокутної системи координат (мал. 2). На цій площині незбуреному руху, очевидно, буде відповідати так називана точка рівноваги або точка спокою системи – початок координат .

Рис. 2

Кожному конкретному збуреному руху, обумовленому збуреннями  й , у кожен даний момент часу t, на площині  буде відповідати деяка точка , називана зображуючою точкою. Із часом точка М буде переміщатися, описуючи деяку траєкторію l, називану фазовою траєкторією, параметричне рівняння якої

 и.

Ця траєкторія починається в точці  з координатами

.

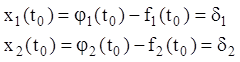Отже, кожному збуреному руху, обумовленому даними значеннями збурень  і  на фазовій площині , буде відповідати певна фазова траєкторія, що починається в точці .

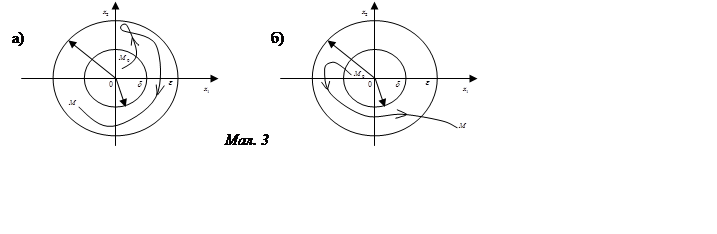
Як говорилося, даний розрахунковий режим роботи динамічної системи (незбурений рух) буде стійким, якщо при досить малих збуреннях режим роботи системи (збурений рух) буде увесь час як бажано мало відрізнятися від розрахункового (незбуреного руху). У цьому випадку всяка фазова траєкторія, що починається в будь-якій точці , досить близької до початку координат, буде цілком належати як завгодно малій околиці початку координат (мал. 3а). Таким чином, переходимо до наступного визначення:

Означення. Незбурений рух (3.2) називають стійким, якщо для кожного, наперед заданого  можна вказати таке  що при будь-яких збурюваннях , , що задовольняють умові  при всіх  буде виконуватися нерівність . У противному випадку рух називають нестійким (мал. 3).

Із множини стійких незбурених рухів виділимо такі розв’язання, до яких асимптотично прагне будь-який збурений рух при досить малих значеннях збурювань так, що

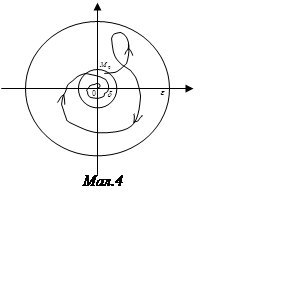Такі стійкі незбурені рухи називаються асимптотично стійкими (мал. 4). Сформулюємо аналогічне визначення стійкості точки спокою для розв’язання  системи  рівнянь. Для цього аналогічно вводимо поняття варіацій   фазового простору й фазових траєкторій. Незбурений рух  називається стійким, якщо для  , що при будь-яких збурюваннях , що задовольняють умові  для  виконується нерівність . У противному випадку рух нестійкий. Якщо рух стійкий і