Теорія стійкості. Критерії стійкості

3.7 Критерії стійкості

3.7.1 Критерій Гурвіца

Нехай для лінійної автономної системи -го порядку характеристичне рівняння має вигляд

,                                  (3.35)

де , . Складемо квадратну матрицю  порядку  (матрицю Гурвіца) у наступним чином. По головній діагоналі матриці  поставимо коефіцієнти . У першому стовпці розташуємо коефіцієнти з непарними індексами, у другому – з парними, починаючи с  Третій і четвертий стовпці будуємо знову з коефіцієнтів відповідно непарних і парних індексів, але тепер перші елементи цих стовпців беремо рівними нулю. У п'ятому й шостому стовпцях ставимо знову коефіцієнти відповідно непарних і парних індексів, але тепер перші два елементи цих стовпців дорівнюють нулю. Таким чином, матриця  має вигляд

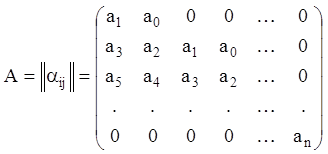,                                                   (3.36)

а її елементи будуються з коефіцієнтів рівняння (3.35) по формулі , причому якщо число  від’ємне, або більше , то приймають . Складемо головні діагональні мінори матриці :

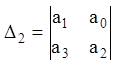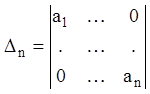, ,…,...                                              (3.37)

Тоді має місце критерій Гурвіца (1859-1919) (теорема доводиться у вищій алгебрі).

Критерій Гурвіца. Для того щоб всі корені алгебраїчного рівняння (3.35) з дійсними коефіцієнтами мали від’ємні дійсні частини, необхідно й досить, щоб всі головні діагональні мінори (3.37) матриці Гурвіца (3.36) були додатними:

                                             (3.36)

З теорем 1-3 про стійкість автономних систем і критерію Гурвіца витікає:

1)  Якщо при  від’ємні всі головні діагональні мінори матриці Гурвіца, складеної для характеристичного рівняння лінійної автономної системи, то нульове розв'язання системи асимптотичне стійке;

2)  Якщо ж хоча б один з розглянутих мінорів від’ємний, то нульове розв'язання системи нестійке.

З формул Вієта для рівняння (3.35)

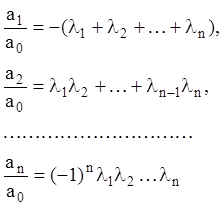                                                (3.39)

маємо, що при  й умови заперечності дійсних частин характеристичних чисел  витікає додатність всіх коефіцієнтів  характеристичного рівняння (3.35), зворотне твердження невірно.

Звідси одержуємо дві пропозиції:

а) для того, щоб при  всі характеристичні числа  мали від’ємні дійсні частини, необхідно (але не досить), щоб всі коефіцієнти рівняння (3.35) були додатні:

;                                                  (3.40)

б) якщо при  хоча б один з коефіцієнтів  від’ємний, то серед характеристичних чисел  є числа з додатною речовинною частиною.

Розглянемо як окремі випадки системи перших чотирьох порядків.

1. Система першого порядку .

Характеристичне рівняння  . Умова асимптотичної стійкості .

2. Система другого порядку .

Характеристичне рівняння  . Записуємо матрицю Гурвіца (3.36) і умову (3.38)

, , ,

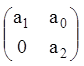звідки одержуємо умову асимптотичної стійкості

, .                                                     (3.41)

3. Система третього порядку .

Характеристичне рівняння  . Матриця й умови Гурвіца

, , , ,

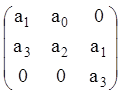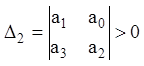звідси одержуємо умову асимптотичної стійкості систем третього порядку

, , , .                             (3.42)

4. Система четвертого порядку .

Характеристичне рівняння  , матриця й умови Гурвіца

,   ,    ,

,    .

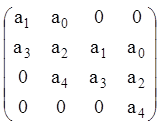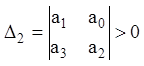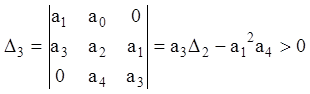Так як 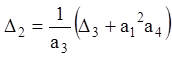, то при від’ємності всіх коефіцієнтів характеристичного рівняння (нерівності (3.40)) з умови  випливають умови  й , таким чином умови  й  тут не є незалежними й можуть бути виключені з розгляду. Тому умови асимптотичної стійкості систем четвертого порядку мають вигляд

, , ,  ,

.                                      (3.41)

Приклад. Установити при якому значенні параметра  асимптотичне стійке нульове розв'язання рівнянь обуреного руху

, , .

Розв’язання. Записуємо характеристичне рівняння

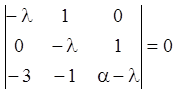, або .

Задовольняючи умовам (3.40), (3.42)одержуємо нерівності

, ,

розв’язанням яких буде .

Відповідь: розв’язання системи асимптотичне стійке при .

9.7. 2 Критерій Л’єнара–Шипара

Аналіз систем третього й четвертого порядків показує, що не всі умови Гурвіца незалежні, а саме: з від’ємності мінорів непарного порядку витікає додатність мінорів парного порядку й навпаки, (ця властивість є загальним для систем довільного порядку ). Воно дозволило французьким математикам Л’єнару й Шипару сформулювати наступний критерій стійкості лінійних автономних систем:

Щоб всі корені рівняння (9.35) мали від’ємні речовинні частини, необхідно й досить виконання двох умов:

1)  повинні бути додатні всі коефіцієнти цього рівняння , ;

2)  повинні бути додатні всі діагональні мінори або непарного, або парного порядку, тобто

 або

.

Звідси очевидно, що критерій Л’єнара-Шипара має деяку перевагу перед критерієм Гурвіца, оскільки він вимагає трохи меншої обчислювальної роботи.

Однак застосування критеріїв такого типу для систем порядку вище четвертого стає практичним неефективним у зв'язку із громіздкістю обчислень визначників високих порядків.

9.7. 3 Критерій Михайлова

В.А. Михайлов в 1938р. розробив графоаналітичний метод дослідження й відповідний критерій стійкості руху. Розглядаємо характеристичне рівняння системи

.                                (3.44)

Якщо  – характеристичні числа, то (3.44) запишеться:

.                                           (3.45)