Нехай ![]() – деяке характеристичне число. На мнимій
осі візьмемо довільну точку
– деяке характеристичне число. На мнимій
осі візьмемо довільну точку ![]() й побудуємо вектор
й побудуємо вектор ![]() із точки
із точки ![]() в точку
в точку
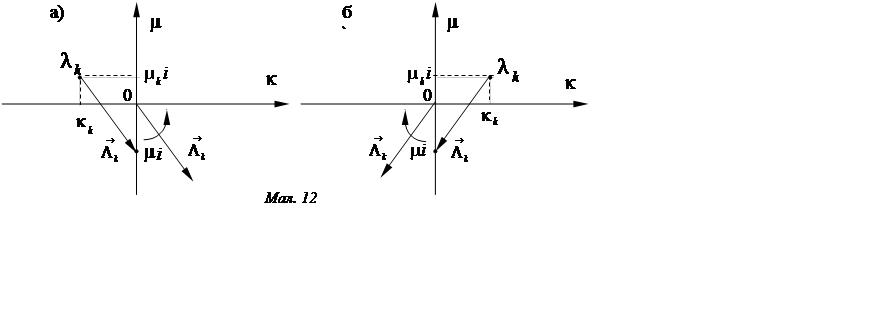
![]() (мал. 12). При неперервній зміні
(мал. 12). При неперервній зміні ![]() від
від ![]() до
до ![]() вектор
вектор ![]() повернеться
навколо початку координат на кут
повернеться
навколо початку координат на кут ![]() проти годинної стрілки
(якщо
проти годинної стрілки
(якщо ![]() , те по годинній стрілці).
, те по годинній стрілці).
Поклавши в характеристичному рівнянні (3.45) ![]() ,
одержуємо:
,
одержуємо:
![]() (3.46)
(3.46)
де ![]() ;
; ![]() ,
, ![]() .
.
 У такий спосіб маємо
функцію комплексної змінної
У такий спосіб маємо
функцію комплексної змінної ![]() . Кожному фіксованому значенню
. Кожному фіксованому значенню
![]() на комплексній площині
на комплексній площині ![]() відповідає деяка фіксована точка
відповідає деяка фіксована точка ![]() або радіус-вектор цієї точки
або радіус-вектор цієї точки ![]() . При неперервній зміні
. При неперервній зміні ![]() кінець вектора
кінець вектора ![]() опише
на площині
опише
на площині ![]() деяку криву
деяку криву ![]() ,
називану годографом Михайлова. Параметричні рівняння годографа
,
називану годографом Михайлова. Параметричні рівняння годографа ![]() мають вигляд:
мають вигляд:
![]() .
.
За початок кривої
приймається точка ![]() дійсної осі. Накладене на
дійсної осі. Накладене на ![]() обмеження
обмеження ![]() (точка
переміщається в площині уздовж мнимої осі від
(точка
переміщається в площині уздовж мнимої осі від ![]() до
до ![]() ) дозволить на підставі аналізу
) дозволить на підставі аналізу ![]() з'ясувати розташування коренів
характеристичного рівняння щодо мнимої осі.
з'ясувати розташування коренів
характеристичного рівняння щодо мнимої осі.
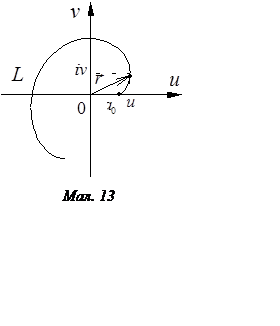 Якщо
всі
Якщо
всі ![]() мають від’ємні речовинні частини, то при
зміні
мають від’ємні речовинні частини, то при
зміні ![]() від
від ![]() до
до ![]() зміна аргументу
зміна аргументу ![]() кожного
співмножника
кожного
співмножника ![]() в (3.46) буде дорівнює в межі
в (3.46) буде дорівнює в межі ![]() (радіус-вектор
(радіус-вектор ![]() , що
відповідає
, що
відповідає ![]() повертається проти годинникової стрілки на
кут
повертається проти годинникової стрілки на
кут ![]() ). Отже, зміна аргументу функції
). Отже, зміна аргументу функції ![]()
![]() буде в межі дорівнює
буде в межі дорівнює ![]() (при множенні в
(при множенні в ![]() комплексних
чисел
комплексних
чисел ![]() їхні аргументи складаються).
їхні аргументи складаються).
Якщо всі ![]() мають додатні дійсні частини, то
зміна аргументу кожного множника
мають додатні дійсні частини, то
зміна аргументу кожного множника ![]() буде в межі дорівнює
буде в межі дорівнює ![]() . Тоді зміна аргументу
. Тоді зміна аргументу ![]() при зміні
при зміні ![]() від
від ![]() до
до ![]() буде
дорівнює
буде
дорівнює ![]() .
.
Якщо ![]() коренів мають додатну речовинну частину, а
коренів мають додатну речовинну частину, а
![]() – , від’ємну то при зміні
– , від’ємну то при зміні ![]() від
від ![]() до
до ![]() зміна аргументу
зміна аргументу ![]()
![]() .
.
Досліджувана система стійка, якщо ![]() , тобто
якщо
, тобто
якщо ![]() .
.
Тому що ![]() – парна функція, її графік
симетричний щодо полярної осі, сполученої з віссю
– парна функція, її графік
симетричний щодо полярної осі, сполученої з віссю ![]() , то
можна обмежитися дослідженням кривої при
, то
можна обмежитися дослідженням кривої при ![]() . Тоді в
загальному випадку зміна аргументу буде дорівнює
. Тоді в
загальному випадку зміна аргументу буде дорівнює
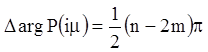 ,
,
для стійкої системи:
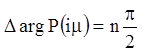 .
.
Звідси випливає Критерій Михайлова:
Для того, щоб всіх корені характеристичного рівняння (3.44) мали
від’ємні дійсні частини, необхідно й досить, щоб при неперервній зміні ![]() від
від ![]() до
до ![]() вектор
вектор ![]() повернувся
проти годинникової стрілки навколо початку координат на кут
повернувся
проти годинникової стрілки навколо початку координат на кут ![]() , де
, де ![]() –
степінь характеристичного многочлена.
–
степінь характеристичного многочлена.
Таким чином, якщо годограф Михайлова ![]() при
зміні
при
зміні ![]() від
від ![]() до
до ![]() , почавшись у т.
, почавшись у т. ![]() ,
пройде всього
,
пройде всього ![]() квадрантів площини
квадрантів площини ![]() (у послідовності: перший, другий, третій,
четвертий, перший, другий і т.д.), той досліджуваний рух асимптотичне стійкий.
(у послідовності: перший, другий, третій,
четвертий, перший, другий і т.д.), той досліджуваний рух асимптотичне стійкий.
 Звідси
витікає, що незбурений рух буде нестійким у наступних випадках:
Звідси
витікає, що незбурений рух буде нестійким у наступних випадках:
1)
якщо число квадрантів площини ![]() , пройдених годографом Михайлова, не
дорівнює порядку
, пройдених годографом Михайлова, не
дорівнює порядку ![]() системи;
системи;
2)
якщо початкова точка годографа ![]() лежить не на від’ємній півосі;
лежить не на від’ємній півосі;
3)
якщо порушується послідовність проходження
квадрантів площини ![]() ;
;
4)
якщо на деяких проміжках зміни ![]() вектор
вектор ![]() обертається
по годинній стрілці:
обертається
по годинній стрілці:
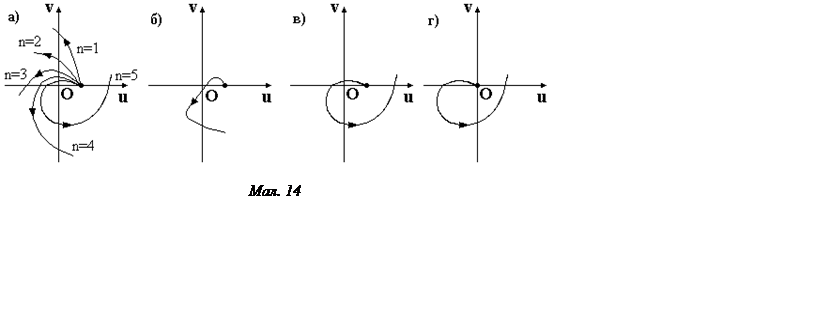
На мал. 14 зображені криві Михайлова, що відповідають стійким системам різних порядків (а), нестійким системам (б), системам, що перебувають на границі стійкості (в, г).
При практичних дослідженнях критерій Михайлова використовують в
алгебраїчному виді, заміняючи годограф Михайлова двома окремими кривими ![]() й
й ![]() . При
цьому критерій Михайлова формулюється так: для того, щоб всіх корені
характеристичного рівняння (3.44) мали від’ємні дійсні частини, необхідно й
досить, щоб многочлени
. При
цьому критерій Михайлова формулюється так: для того, щоб всіх корені
характеристичного рівняння (3.44) мали від’ємні дійсні частини, необхідно й
досить, щоб многочлени ![]() й
й ![]() мали в
сукупності всього
мали в
сукупності всього ![]() дійсних, від’ємних коренів і щоб
у послідовності цих коренів, записаних у порядку їхнього зростання, за кожним
коренем многочлена
дійсних, від’ємних коренів і щоб
у послідовності цих коренів, записаних у порядку їхнього зростання, за кожним
коренем многочлена ![]() йшов корінь многочлена
йшов корінь многочлена ![]() , і навпаки.
, і навпаки.
Приклад 1. Дослідити
стійкість нульового розв’язання диференціального рівняння ![]() .
.
Розв’язання: Записуємо характеристичний многочлен:
![]() .
.
Заміняємо в ![]()
![]() на
на ![]() :
:
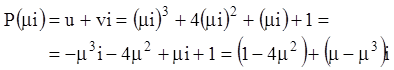 .
.
Звідси одержуємо
параметричні рівняння годографа Михайлова ![]() :
: ![]() . Знаходимо точки перетинання кривій
. Знаходимо точки перетинання кривій ![]() осей координат. Із цією метою знаходимо
корінь многочленів
осей координат. Із цією метою знаходимо
корінь многочленів ![]() й
й ![]() ,
розв’язав рівняння:
,
розв’язав рівняння:

![]() .
.
Беремо тільки від’ємні
корені цих рівнянь, тому що будується половина годографа, що відповідає зміні
параметра ![]() від
від ![]() до
до ![]() . Такими коріннями, розташованими в порядку
зростання, будуть
. Такими коріннями, розташованими в порядку
зростання, будуть 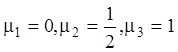 . Записуємо в таблицю ці корені і
відповідні їм значення
. Записуємо в таблицю ці корені і
відповідні їм значення ![]() й
й ![]() .
.
Таким чином, крива
Михайлова, починається в точці ![]() осі
осі ![]() , проходить перший квадрант, входить у
другий у точці
, проходить перший квадрант, входить у
другий у точці 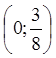 , проходить другий квадрант,
входить у третій у точці
, проходить другий квадрант,
входить у третій у точці ![]() . Знайдемо граничні
значення тангенса кута, утвореного вектором
. Знайдемо граничні
значення тангенса кута, утвореного вектором ![]() з віссю
з віссю
![]() або
або ![]() :
:
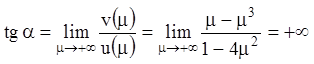 .
.
Тоді ![]() . Значить годограф Михайлова, не виходячи
із третього квадранта, опускається в нескінченність.
. Значить годограф Михайлова, не виходячи
із третього квадранта, опускається в нескінченність.
Висновок: годограф Михайлова, почавшись у точці
додатної півосі ![]() , послідовно пройшов три
квадранти площини
, послідовно пройшов три
квадранти площини ![]() (у порядку перший, другий,
третій), у результаті чого вектор
(у порядку перший, другий,
третій), у результаті чого вектор ![]() повернувся на кут
повернувся на кут ![]() . Звідси в силу критерію Михайлова робимо
висновок, що всі корені характеристичного рівняння мають від’ємні дійсні
частини, тобто нульове розв’язування досліджуваного рівняння асимптотичне
стійке.
. Звідси в силу критерію Михайлова робимо
висновок, що всі корені характеристичного рівняння мають від’ємні дійсні
частини, тобто нульове розв’язування досліджуваного рівняння асимптотичне
стійке.
Інший спосіб:
Розв’язання першого рівняння ![]()
![]()
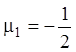 ,
, 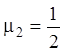 . Розв’язання другого рівняння
. Розв’язання другого рівняння ![]()
![]()
![]() ,
,
![]() . Записавши корені многочленів
. Записавши корені многочленів ![]() й
й ![]() у
порядку зростання
у
порядку зростання
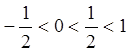 ,
,
бачимо, що за кожним коренем многочлена ![]() йде корінь многочлена
йде корінь многочлена ![]() й навпаки. Виходить, корені рівняння мають
від’ємні дійсні частини й розв’язання досліджуваного рівняння асимптотичне
стійке.
й навпаки. Виходить, корені рівняння мають
від’ємні дійсні частини й розв’язання досліджуваного рівняння асимптотичне
стійке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.