Потрійні інтеграли. Заміна змінних у потрійному інтегралі

Лекція 5

ПОТРІЙНІ ІНТЕГРАЛИ

План:

 5.1. Задача, яка приводить до поняття потрійного інтегралу.

 5.2. Визначення, властивості і обчислення потрійного інтегралу.

 5.3. Заміна змінних у потрійному інтегралі.

 5.4. Узагальнення поняття інтеграла.

 5.5. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1.Потрійний інтеграл обчислюється по якійсь області (просторовій фігурі) заданій в трьохвимірному просторі. Ця фігура обмежена поверхнями, а тому знання рівнянь і вигляду поверхонь  для засвоєння теми “Потрійні інтеграли” є основополагаючим. Подамо рівняння, вигляд і характеристику поверхонь другого порядку, які найчастіше зустрічаються при обчисленні потрійних інтегралів.

1.1.  Циліндричні поверхні – поверхні утворені рухои твірної по якійсь напрямній лінії.

 В залежності від виду напрямної (круг, еліпс, парабола, гіпербола ) і циліндри називаються круговими, еліптичними , параболічними (на рисунку б), гіперболічними (на рисунку а).

Рівняння циліндрів за виглядом співпадають з рівнянням кривої, яка є напрямною для руху твірної. Яка координата в рівнянні циліндра відсутня – тій вісі і будуть паралельні твірні.

1.2. Конічні поверхні утворюються коли закріплена в одній точці (ця точка зветься вершиною конуса) твірна рухається по напрямній.

Ми розглядаємо, як правило, конуси кругові, або елптичні з вершиною на початку координат (як на рисунку), або розташованою в довільній точці на вісі симетрії. Рівняння кругового конуса:  – вершина в точці О(0,0,0), вісь симетрії – Оz. Для конуса   – вершина в точці С(0,0, с). Перетин цього конуса площиною  паралельною координатній площині хОу дасть коло, рівняння проекції якого на площину хОу буде: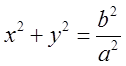. Перетин площиною не паралельною хОу дасть еліпс як це зображено на рисунку. 

Рівняння еліптичного конуса 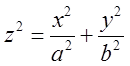. Перетин цього конуса площиною  дасть еліпс.

1.3.Еліпсоїдні поверхні одержуються від обертання  еліпса (еліпсоїд обертання), або від деформації сфери (еліпсоїд деформації).

Рівняння еліпсоїда 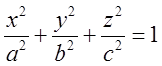. Цей еліпсоїд різноосний, в чому легко переконатись зробиши перетин його координатними площинами . В перетині ми одержимо еліпси з різними напівосями. Еліпси в перетині утворяться не лише при перетині еліпсоїда координатними площинами, а й їм паралельними. Якщо , то одержимо найдосконалішу поверхню в природі – сферу. Перетин сфери з як завгодно розташованою площиною є коло. Але проекції кола, яке ми одержуємо при перетині з площиною, на координатні площини – будуть еліпсами. Перетин сфери з круговим конусом також дасть коло.

1.4.Гіперболоїдні поверхні утворюються при обертанні гіперболи навколо однієї із осей координат.

Якщо гіперболу 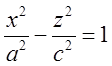обертати навколо вісі, яка її не перетинає (в даному разі Oz), то одержимо, так званий, однопорожнинний гіперболоїд обертання 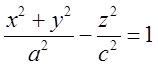 . Якщо ми його деформуємо вздовж третьої координатної вісі (в даному разі Оу), то одержимо   (на рисунку а) однопорожнинний гіперболоїд загального виду 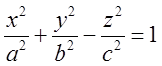. Перетин цієї поверхні площиною паралельною координатній хОу дасть еліпс.

                   а)                                            б)                          На рисунку б) зображено  двопорожнинний гіперболоїд. Його загальне (деформований) рівняння  має в собі два знаки “–“: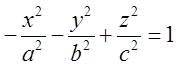 на відміну від попереднього однопорожнинного – де знак “–” – один. Це полегшує запамятовування рівнняння і назву.

1.5. Параболоїдні поверхні утворюються при рухові однією параболи вершиною по іншій із збереженням осей   парабол паралельними одній із осей координат.  На рис.а) і б) зображена побудова гіперболічного параболоїда: по нерухомій параболі  рухається парабола , як бачимо параболи напрямлені в протилежні сторони.

 Одержуємо рівняння гіперболічного  параболоїда 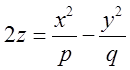 . Цю поверхню   прозвали “сідло” за її схожівсть до відповідного елементу збруї наших славних предків – Запоріжських козаків, хоч вони й гадки не мали про гіперболічний параболоїд. Рівняння цієї поверхні не завжди дається в канонічному вигляді, а  буває і в такому: . Це те ж саме сідло, але повернуте на  навколо вісі Oz.

            Простішою в побудові є поверхня параболоїда обертання, коли парабола  (або ) обертається навколо своєї вісі Oz – рисунок в). В обох випадках одержимо рівняння параболоїда обертання . В перетині цієї поверхні площиною z=h, парлельною координатній площині хОу, одержимо коло, рівняння проекції якого на координатну площину хОу буде: .

Цей параболоїд можна також одержати рухом параболи по парболі (чи навпаки, рис.г)). Звернніть увагу, що параболи мають однакову направленість. Якщо цей параболоїд

обертання піддамо деформації, то одержимо