Остання формула виражає фізичне тлумачення потрійного
інтеграла. Геометричного тлумачення цей тип інтеґрала не має, оскільки немає
геометричного тлумачення чотиривимірної системи координат. Теорема існування
такого інтеґрала крім неперервності в області
підінтеґральної функції також вимагає скінченності області
інтеґрування. Область ми будемо називати правильною, якщо перетинаюча
її пряма паралельна осі ОХ (відповідно ОУ та OZ) перетинає її поверхню лише
в двох точках – в одній точці входить в область і в одній виходить з неї. Обчислення
потрійного інтеґрала, у випадку правильності відповідних областей (таких, як на рис. 5.1)
зводиться до обчислення трьох одновимірних інтегралів. Правильна
трьохвимірна область V (рис.5.1)
може бути спроектована на площину ХОУ в правильну двох вимірну область D. Ця двохвимірна область може бути
спроектована на вісь ОХ у виді відрізка з початком в точці ![]() і кінцем в точці
і кінцем в точці ![]() .
Якщо рівняння кривих, які обмежують область D,
.
Якщо рівняння кривих, які обмежують область D, ![]() – нижня крива та
– нижня крива та ![]() –
верхня крива, то маємо формулу для обчислення потрійного інтегралу
–
верхня крива, то маємо формулу для обчислення потрійного інтегралу
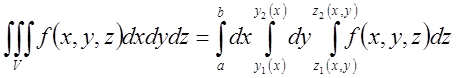 (5.3)
(5.3)
Звичайно, ця формула симетрична, тобто зовнішній інтеграл можна взяти по у середній по z, внутрішній по х. Інтегрувати можна в любому порядку. Цей порядок ми обираємо самі в залежності від виду області та підінтегральної функції.
Властивості потрійного інтеграла аналогічні властивостям подвійного.
1) )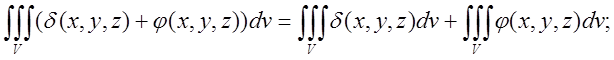 (5.4)
(5.4)
2) 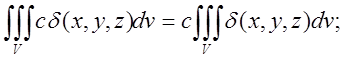 (5.5)
(5.5)
3) 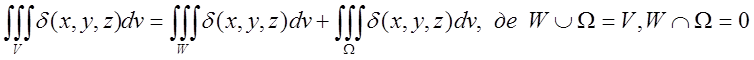 (5.6)
(5.6)
4)![]()
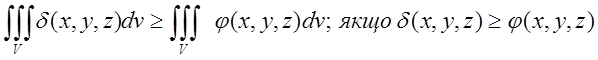 (5.7)
(5.7)
5) 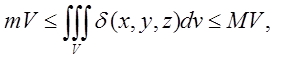 де V – об’єм ,
де V – об’єм , ![]() (5.8)
(5.8)
6) Теорема про середнє значення: 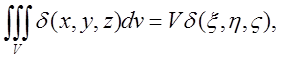 де
де ![]() (5.9)
(5.9)
П.1.Оцінити інтеграл
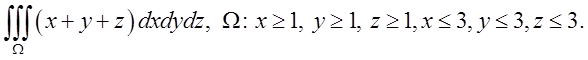
Розв’язок. Оцінювати будемо за
(5.8). Обєм куба ![]() . Найменше значення
підінтегральної функції в цьому кубові буде в точці (1,1,1)
. Найменше значення
підінтегральної функції в цьому кубові буде в точці (1,1,1) ![]() . Найбільше значення підінтегральної
функції в цьому кубові буде в точці (3,3,3)
. Найбільше значення підінтегральної
функції в цьому кубові буде в точці (3,3,3) ![]() , А тому
, А тому
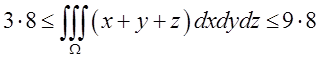 .
.
П.2. Розставити границі інтегруваня в потрійному
інегралі 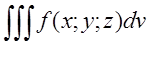 де V-область обмежена площинами x+2y+3z=6
;x=0; y=0;
z=0;
де V-область обмежена площинами x+2y+3z=6
;x=0; y=0;
z=0;
Розв’язок :
Зобразимо область на рисунку , перетворивши рівняння площини у рівняння у відрізках: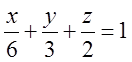 . Рівняння прямої АВ на площині хOу має вид
. Рівняння прямої АВ на площині хOу має вид 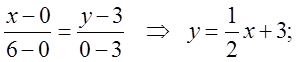 Зовнішній
інтеграл беремо вздовж осі ОХ. Очевидно, що 0
Зовнішній
інтеграл беремо вздовж осі ОХ. Очевидно, що 0![]() ; середній інтеграл беремо за змінною у. Щоб
визначити межі в яких змінюється у при 0
; середній інтеграл беремо за змінною у. Щоб
визначити межі в яких змінюється у при 0![]() , беремо на відрізку
, беремо на відрізку ![]() довільну
точку N і проводимо через неї пряму паралельну осі у.
Довжина відрізка NM і буде довжиною по якій ми інтегруємо за у-ком.
Нижній кінець (точна N) цього відрізка на площині має координати
довільну
точку N і проводимо через неї пряму паралельну осі у.
Довжина відрізка NM і буде довжиною по якій ми інтегруємо за у-ком.
Нижній кінець (точна N) цього відрізка на площині має координати ![]() ; а верхній – (точка М)
; а верхній – (точка М) 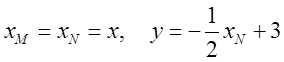 . Таким чином межі середнього інтеграла будуть
. Таким чином межі середнього інтеграла будуть 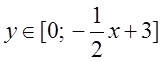 . Щоб визначити межі інтегрування за
змінною z, на відрізку NM візьмемо
довільну точку Q. Проведемо через неї пряму паралельну осі z. Ця пряма перетне нашу область V в двох
точках Q i K. В точці Q вона ввійде в область, а в точці K вийде з неї. Відрізок QK і буде відрізком інтегрування за змінною z. Очевидно в просторі координати точки Q
будуть:
. Щоб визначити межі інтегрування за
змінною z, на відрізку NM візьмемо
довільну точку Q. Проведемо через неї пряму паралельну осі z. Ця пряма перетне нашу область V в двох
точках Q i K. В точці Q вона ввійде в область, а в точці K вийде з неї. Відрізок QK і буде відрізком інтегрування за змінною z. Очевидно в просторі координати точки Q
будуть: 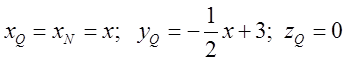 . Координати точки K на
площині будуть:
. Координати точки K на
площині будуть: 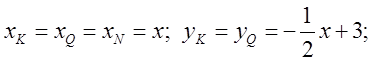 просторову
координату z треба знаходити з умови, що точка К лежить на
площині
просторову
координату z треба знаходити з умови, що точка К лежить на
площині 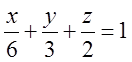 і, якщо дві координати х і у уже
визначені, то з рівняння площини
і, якщо дві координати х і у уже
визначені, то з рівняння площини 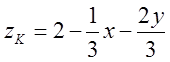 .
Таким чином
.
Таким чином 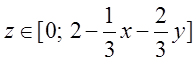 .
.
Розставляючи границі інтегрування мислимо
слідуючим образом. Якщо х буде змінюватись від 0 до 6 , а точка Q , буде “бігати” вздовж відрізка MN від N до M, то тоді Q
побуває в кожній точці області обмеженої трикутником АОВ, а точна К побуває в
кожній точці області, обмеженої трикутником АВС, а тому: 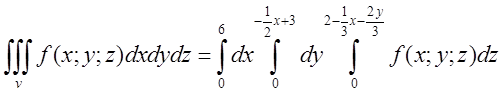 .
.
П.3 Обчислити 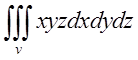 , де V область обмежена поверхнями
, де V область обмежена поверхнями ![]()
Область V є трикутна піраміда з основою АВО, у якої бічна грань АОС вигнута
поверхня z=xy.
Обчислюючи цей інтеграл, всю фігуру зображувати не обов’язково.
Границі інтегрування по z задані в умові в явному виді ![]() . Границі інтегрування по у теж задані в
умові
. Границі інтегрування по у теж задані в
умові ![]() . Лише для змінної х маємо одне
значення, а тому побудуємо на площині хОу область інтегрування. Нею є
трикутник ОАВ, рівняння сторін якого будуть: ОА: у=0; ОВ: у=х; АВ: х=2.
Звідси добре видно, що
. Лише для змінної х маємо одне
значення, а тому побудуємо на площині хОу область інтегрування. Нею є
трикутник ОАВ, рівняння сторін якого будуть: ОА: у=0; ОВ: у=х; АВ: х=2.
Звідси добре видно, що ![]() .
.
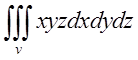
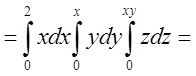
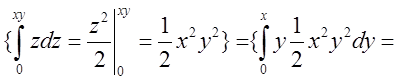
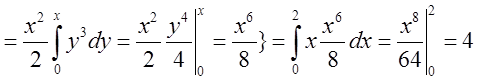 . Відповідь 4
. Відповідь 4
5.3. Заміна змінних у потрійному інтегралі.
Криволінійні (циліндричні й сферичні) координати
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.