Потрійні інтеграли. Заміна змінних у потрійному інтегралі, страница 4

При роботі токарних станків деталі, які підлягають обробці крутяться навколо своєї вісі, радіолокатор веде огляд простору також обертаючись навколо своєї вісі і визначає координати об’єкта не в прямокутній системі координат, а в криволінійній.  При дослідженні руху рідини в циліндричних трубах або руху повітряних мас в колоземному шарі атмосфери використовувати прямокутну систему нераціонально.  Декартова система координат не завжди зручна. Через те поряд з декартовою застосовують інші ортогональні системи координат, найпоширенішими серед яких є циліндрична та сферична.

Система координат називається ортогональною, якщо в кожній точці простору координатні поверхні попарно перпендикулярні.

Координатними поверхнями циліндричної системи є циліндр  і площини , тобто вона є ніби поєднанням полярної системи на площині хОу та декартової в напрямі осі Оz. Циліндрична й декартова системи зв'язані з формулами .

При заміні змінних в потрійному інтегралі і переході до циліндричної системи координат елементарний об’єм  можна розглядати (рис.5.2) як , але ж ми знаємо

                          Рис.5.2                           що при переході до полярної системи  , а тому формула заміни  прямокутних декартових координат на циліндричні в потрійному інтегралі має вид

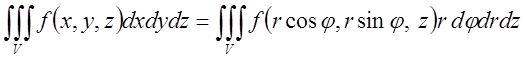                                                       (5.10)

Однозначно визначити положення точки М в трьохвимірному просторі можна, задаючи й інші три характеристики його положення, наприклад: віддаль від початку координат О до точки М і які не-будь два кути між напрямком з фіксованими вісями і напрямком радіус-вектора ОМ. Так вводиться сферична система координат.

                                                            

                         а)                                                                                            б)

Рис.5.3

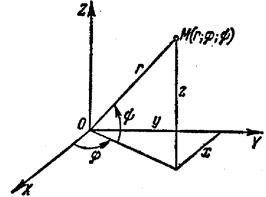
            На рис.5.3 а) прямокутні декартові координати замінюються на віддаль r від початку координат О до точки М, кут  між напрямком ОМ і площиною ХОУ, кут  між віссю ОХ і проекцією відрізка ОМ на площину ХОУ. Зв’язок між координатами систем такий: .                                                        (5.11)

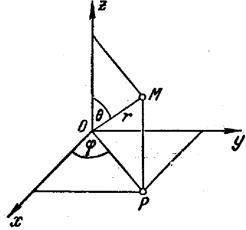
На практиці і в науковій літературі зустрічається система координат (рис.5.3 б)) в якій за координату береться кут між ОМ і віссю ОZ. Зв’язок між координатами систем прямокутної і сферичної такий: .                    (5.12)

 Ми будемо вважати відмінності між (5.11) і (5.!2) не принциповими бо замінивши в (5.12)  прийдемо до (5.11).

Обчислимо якобіан переходу від прямокутної системи до сферичної в формі (5.12).

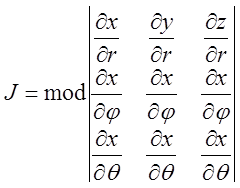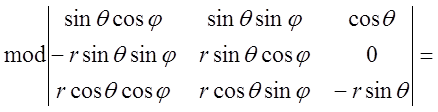
=                       (5.13)

Для заміни по формулах (5.11) якобіан одержимо з (5.13), поклавши .

                                                                                             (5.14)

Таким чином, формула заміни змінних для сферичних координат має вид:

При   

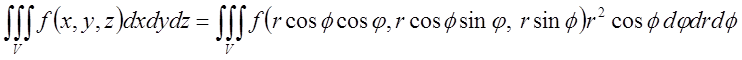                        (5.15)

При

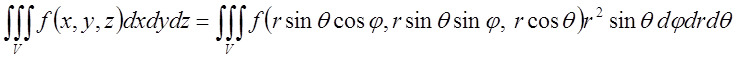                        (5.16)

Як приклад застосування  криволінійних координат у просторі розвяжемо задачу з збірника задач з математичного аналізу для ВТУЗів під ред Демідовича Б.П. № 2249.

Обчислити: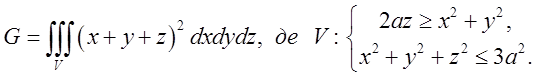

Розвязок. Побудуємо область. Вона має вид зображений на рис.

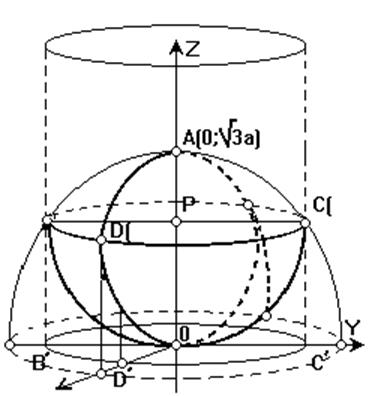Сфера з параболоїдом перетинаються по колу BDC.

Його проекція на площину ХОУ буде коло . Знайдемо його рівняння. Центр кола лежить на початку координат, а тому рівняння матиме вид , де r радіус, який треба знайти. Це зробимо так: Точка С є точка перетину трьох поверхонь – параболоїда, сфери і площини х=0, а значить її координати є розв’язком системи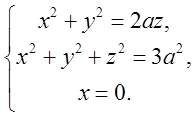

Розв’язком  цієї системи є дві точки  . Перший набір це координати точки В. Другий – координати точки С. Координати точки  будуть:

Але ж , тому рівняння кола буде . Виходячи з виду області інтегрування бачимо, що обчислення будуть раціональніші, якщо ми перейдемо до циліндричної або сферичної системи координат. Яку ж вибрати?. При переході до сферичної с/к інтеграл прийдеться розбивати на два бо верхня границя по r вздовж кола BDC при зміні  буде переходити з поверхні параболоїда на поверхню сфери, крім того громіздким буде вираз під внутрішнім інтегралом. А тому перейдемо до циліндричної с/к. Границі інтегрування по  і по  – очевидні:

. Z змінюється від рівняння параболоїда до рівняння сфери, які ми зараз переведемо в циліндричну с/к.