Потрійні інтеграли. Заміна змінних у потрійному інтегралі, страница 2

поверхню еліптичного параболоїда 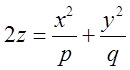, названого так тому, що при перетині цієї поверхні площиною  в перетині одержимо еліпс. Без деформації еліптичний параболоїд одержується рухом параболи  ,  (див. рис. г))

поверхню еліптичного параболоїда ,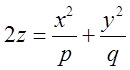

названого так тому, що при перетині цієї поверхні площиною  в перетині одержимо еліпс. Без деформації еліптичний параболоїд одержується рухом параболи  ,  (див. рис. г))

по параболі .

5.1. Задача, яка приводить до поняття потрійного інтегралу

Нехай деяке просторове тіло займає тривимірну область V рис.5.1. Густина  речовини цього тіла в точці  є функція координат цієї точки, тобто .

При умові, що область V обмежена заданими поверхнями: знизу – , згори –  і вертикальна пряма, яка перетинає область V  перетинає ці поверхні лише по одному разу, знайти масу тіла.

           Рис.5.1.                 Для розв’язку цієї задачі застосуємо  метод міркувань, який привів нас до поняття одновимірного і подвійного інтеграла.

Розіб’ємо тіло на елементарні паралелепіпеди площинами паралельними координатним площинам. Виділимо точку   , яка є перетином трьох площин  та . Ці три площини разом з сусідніми площинами ,  та  утворять елементарний паралелепіпед об’єм якого (він зображений на рисунку 5.1. Для аналогії можете уявити як з великої дерев’яної колоди випилюють кубики для дитячої азбуки). Так як цей елементарний паралелепіпед досить маленький і при ,  ,  стягується в точку, то природно  вважати, що густина в ньому є величина постійна і рівна . Маса цього елементарного паралелепіпеда буде дорівнювати . Щоб знайти масу  всього тіла треба знайти суму мас всіх елементарних паралелепіпедів. А для цього нам треба знайти кількість площин паралельних площині xoz, які ділять тіло на шари (якщо роблять кубики, то колоду пропускають через пилораму і кожен шар це є звичайна дошка ). Помножить цю суму на  кількість площин паралельних площині zoу, які разом з попередніми площинами, ділять тіло на паралелепіпеди (не розсипаючи розпиляну на дошки колоду, пропускають її ще раз через пилораму в площині перпендикулярній до попередньої площини і одержують рейки). І, накінець, цей добуток треба помножити на кількість площин паралельних площині xoу, які разом з попередніми площинами, ділять тіло на елементарні паралелепіпеди (не розсипаючи розпиляну на рейки колоду, пропускають її ще раз через пилораму в перпендикулярній до її вісі  площині і одержують кубики). Звичайно, ця сума мас  визначить масу всього тіла приблизно. Точність буде залежати від розмірів елементарних паралелепіпедів: чим меншими вони будуть тим точніше буде враховано зміну густини речовини тіла і точніше ступінчата поверхня тіла буде наближена до істинної. А тому точне значення маси буде потрійна границя при  , ,. Якщо вважати що площини, якими ми розтинали тіло можуть бути віддаленими одна від одної на різні відстані то процес треба розглядати при    , ,.

Зрозуміло, що при цьому кількість  елементарних паралелепіпедів буде прямувати до нескінченності.     

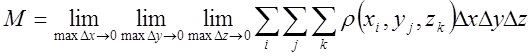                                          (5.1)

5.2. Визначення, властивості і обчислення потрійного інтегралу

 Вираз (5.1) і називають потрійним інтегралом від функції  в області V.

Очевидно, що для існування (5.1) потрібно щоб  в області V була неперервною і скінченною, тобто щоб вона в кожній точці  V приймала якесь конкретне значення.

За аналогією з одно і  двохвимірними інтегралами трьохвимірний, тобто потрійний позначають так

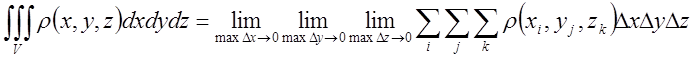                           (5.2)