Подвійні інтеграли. Задачі, що приводять до поняття подвійного інтнграла. Означення і властивості подвійного інтегралу

Лекція 4

ПОДВІЙНІ ІНТЕГРАЛИ

План:

 4.1. Задачі, що приводять до поняття подвійного інтнграла.

 4.2. Означення і властивості подвійного інтегралу.

 4.3. Обчислення подвійного інтеграла.

 4.4. Заміна змінних у подвійному інтегралі.

 4.5. Приклади.

 4.6. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1.Подвійний інтеграл обчислюється по якійсь області заданій на площині хОу, обмеженій лініями, а тому знання рівнянь і вигляду кривих ліній для засвоєння теми “Подвійні інтеграли” є основополагаючим. Подамо рівняння, вигляд і характеристику кривих, які найчастіше зустрічаються в подвійних інтегралах.

1.1.Еліпси. 

На рисунку еліпс, рівняння якого . Розв’язуючи його відносно змінної у, одержимо рівняння верхньої половинки 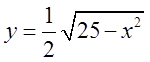 і нижньої половинки 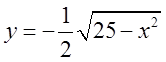. А коли рівняння розв’яжемо відносно змінної х, то одержимо рівняння правої половинки  і лівої половинки. Коло ми розглядаємо, як частинний випадок еліпса (рівні напівосі).

1.2.Параболи квадратичні.

Напрямок віток параболи залежить від знаку перед : якщо знак +, то вітки напрямлені вгору; якщо знак –, то вітки напрямлені вниз. Парабола перетинає вісь Ох в точках, які є коренями рівняння у=0. На рисунку в параболи 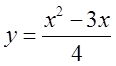 корені .

1.3.Параболи кубічні.

Якщо в кубічній параболі  знак при  стоїть +, то пр зміні х від  до  так же змінюється і у , тобто характер зміни у буде такми, як на рисунку.  Графік кубічної параболи завжди один раз перетинає вісь Оу, і один, або три рази перетинає вісь Ох.

1.4. Графік функції 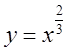 вісь Он має за вісь симетрії, а тому знаходчи обернену функцію (виражаємо х як функцію у) будьмо уважні. Невірно буде просто піднести обидві частини до степеня  і одержати 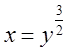. Це буде рівняння лише правої вітки. Вірно буде так: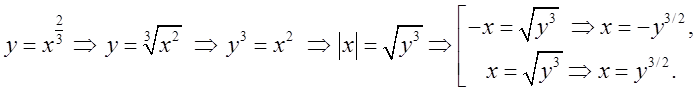 

1.5. Гіпербола (шкільна).

Якщо в рівняння гіперболи 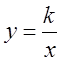 при к>0, знаки біля х і у однакові , то вітки її графіка знахлдяться в І і ІІІ чвертях площини і центр знаходиться в точці О(0,0). Якщо рівняння має вид 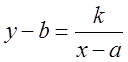, то центр буде в точці  . Наприклад  .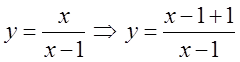

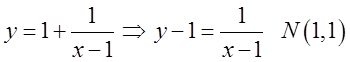1.6. Гіпербола (канонічна).

При вираженні змінних х чи у з канонічного рівняння гіперболи 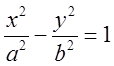, потрібно (як і у випадку з еліпсом) памятати, що ми повинні одержати рівняння двох віток. Наприклад, з рівняння  одержимо рівняння нижніх двох напіввіток 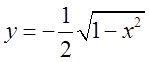 і верхніх .

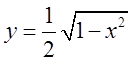1.7. Дробнораціональні функції.

Якщо знаменник функції 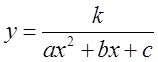 не дорівнює нулю ні при яких значенняз х. То графік цієї кривої буде схожий на профіль степової могили (рос. курган) і при k>0 лежатиме вище вісі Ох, а при k<0 – нижче. Нариклад 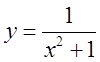 графік на рисунку. Графік функції 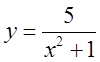 відрізнятиметься лише висотою. 

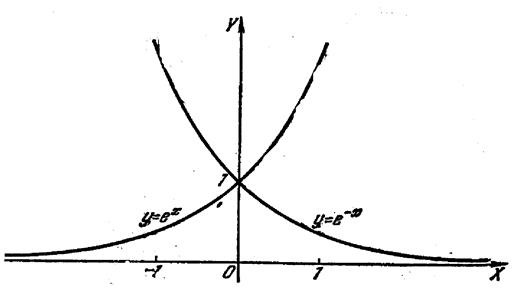
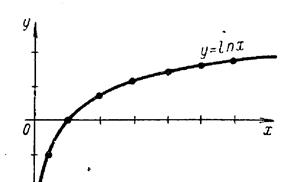
1.8.Показникові та логарифмічні функції.

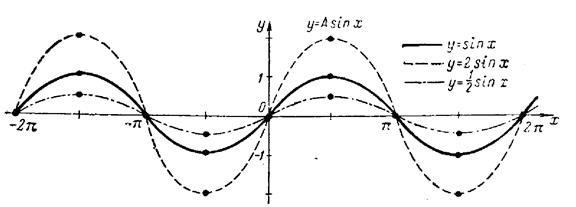
1.9.Тригонометричні функції  

Залежність вигляду графіка функції від зміни аргумента добре видно на рисунках. У звязку з тим, що 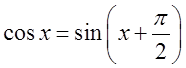, то при побудові графіків функціїї косинуса  виконуються такі ж перетворення лише вісь Оу буде зміщена на  вправо від 0.

1.10. Графіки головних значень обернених тригонометричних функцій.

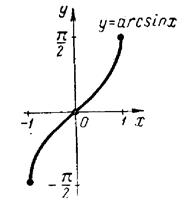
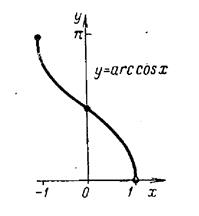
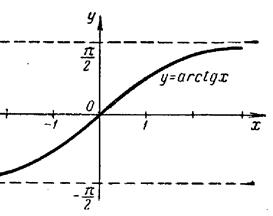
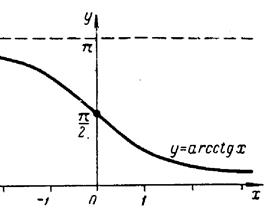
1.11.Рівняння і графіки деяких цікавих кривих, побудувати які можна в полярній системі координат, або застосовуючи параметр.

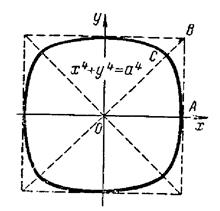
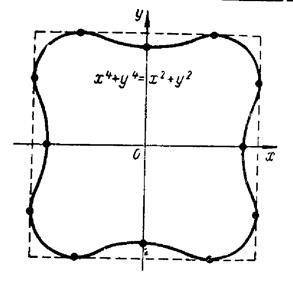
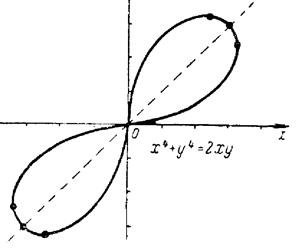
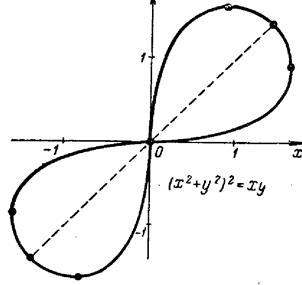
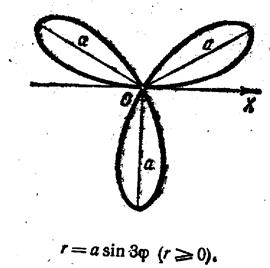
                                                     Трипелюсткова                    Чотирьохпелюсткова

                                                             троянда                                троянда 

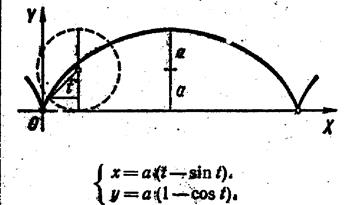
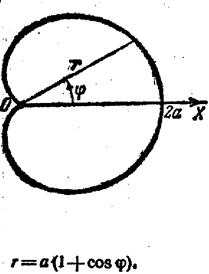
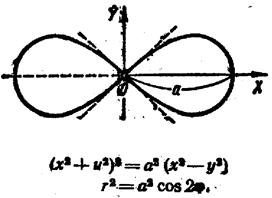
                  Циклоїда                           Кардіоїда                          Лемніската Бернулі

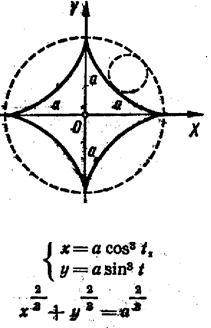
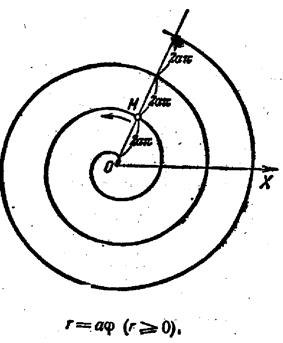
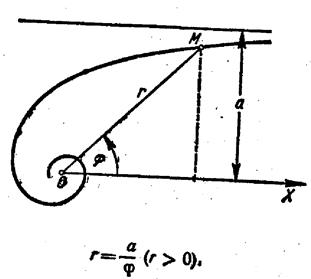
 Гіпоциклоїда               Спіраль Архімеда                      Гіперболічна спіраль

   (астроїда)

Логарифмічна спіраль

2. При знаходженні точок перетину двох ліній треба розвязати систему з двох рівнянь яими описуються ці лінії.