за умови, що вона не залежить від
способу розбиття області D на частини та вибору точок ![]() ),
в кожній частині області.
Згідно з (4.4), для (4.2) і (4.3) маємо V =
),
в кожній частині області.
Згідно з (4.4), для (4.2) і (4.3) маємо V =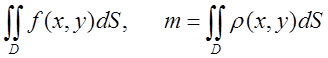 Ці
формули виражають відповідно геометричне й фізичне тлумачення подвійного
інтеґрала. Неперервність підінтеґральної функції забезпечує існування
інтеґрала. Зазначимо, що, скориставшись, можливістю довільності розбиття
області D і виконавши таке розбиття прямими,
паралельними координатним осям, дійдемо висновку, що в (4.4), а отже, і далі,
можна замість dS писати dxdy.
Ці
формули виражають відповідно геометричне й фізичне тлумачення подвійного
інтеґрала. Неперервність підінтеґральної функції забезпечує існування
інтеґрала. Зазначимо, що, скориставшись, можливістю довільності розбиття
області D і виконавши таке розбиття прямими,
паралельними координатним осям, дійдемо висновку, що в (4.4), а отже, і далі,
можна замість dS писати dxdy.
З метою
компактних записів та узагальнення відповідних результатів, у подальшому
ототожнюватимемо (![]() ) з певною точкою, наприклад
) з певною точкою, наприклад ![]() ,. Властивості подвійного інтеґрала
аналогічні властивостям одновимірного інтеграла, а тому приведемо їх без
доведення. Читач, використовуючи геометричне тлумачення, зможе легко
в них переконатися.
,. Властивості подвійного інтеґрала
аналогічні властивостям одновимірного інтеграла, а тому приведемо їх без
доведення. Читач, використовуючи геометричне тлумачення, зможе легко
в них переконатися.
І. Лінійність (адитивність за функцією та однорідність) функціонала подвійного інтегрування ;
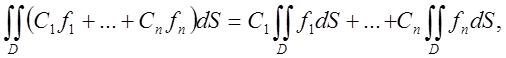
![]()
2.Адитивність за областю інтегрування 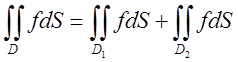
![]() площа
площа![]()
3. Інтегрування нерівності 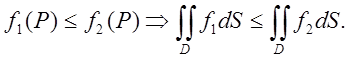
4. Оцінка інтеграла 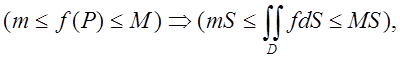 (S – площа D, m – найменше, M – найбільше значення
функції в області).
(S – площа D, m – найменше, M – найбільше значення
функції в області).
5. Теорема про середнє значення 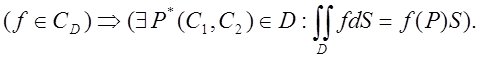
Як і для визначеного інтеґрала, для подвійного інтеґрала існує дві схеми застосування. Перша базується на його означенні як границі інтегральної суми, друга використовує знаходження диференціала шуканої величини, який потім інтеґрують.
Вище ми ввели означення
подвійного інтеграла в самому загальному виді. Але ця загальність не порушилась
би коли б ми розбили довільним способом D на частини, а значить відповідним
чином весь об'єм, площинами паралельними координатним площинам xoz i yoz на суму елементарних об'ємів
(рис. 4.1). Тоді б ![]() , – площа частини області D, а
, – площа частини області D, а ![]() – висота “елементарного
паралелепіпеда”. Ми її вважатимемо постійною в межах зміни х,у в
– висота “елементарного
паралелепіпеда”. Ми її вважатимемо постійною в межах зміни х,у в ![]() . Об’єм елементарного паралелепіпеда
. Об’єм елементарного паралелепіпеда
![]()
![]()
Об’єм всієї фігури приблизно дорівнює сумі
всіх ![]() . Суму прийдеться знаходити
так: спочатку знайти суму від кількості розбиття по змінній х (за індексом і,
це буде кількість шарів), а потім по змінній у (за індексом j, це буде кількість елементарних
паралелепіпедів в кожному шарі ).
. Суму прийдеться знаходити
так: спочатку знайти суму від кількості розбиття по змінній х (за індексом і,
це буде кількість шарів), а потім по змінній у (за індексом j, це буде кількість елементарних
паралелепіпедів в кожному шарі ). 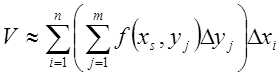 . Зауважимо, що
величина цього об’єму не залежить від порядку обчислення суми, тобто можна
індекси переставити місцями (знаходити кількість шарів за змінною у, а потім
кількість елементарних паралелепіпедів в кожному шарі). Але величина об’єму
залежить від величин
. Зауважимо, що
величина цього об’єму не залежить від порядку обчислення суми, тобто можна
індекси переставити місцями (знаходити кількість шарів за змінною у, а потім
кількість елементарних паралелепіпедів в кожному шарі). Але величина об’єму
залежить від величин ![]() . Чим вони менші тим приблизне
значення об’єму буде ближче до істинного, а це значить, що точне значення
об’єму є границя від приблизного при наближенні найбільших значень
. Чим вони менші тим приблизне
значення об’єму буде ближче до істинного, а це значить, що точне значення
об’єму є границя від приблизного при наближенні найбільших значень ![]() до 0
до 0
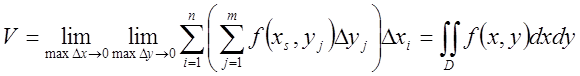 (4.4а)
(4.4а)
4.3. Обчислення подвійного інтеграла
Конструкція (4.4а)
наштовхує нас на думку, що при обчислені подвійного інтеграла треба його звести
до внутрішнього одновимірного інтегралу і зовнішнього (як в (4.4а) стоять
внутрішня сума і зовнішня). Реалізуємо нашу догадку для обчислення 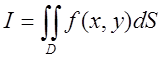 за умови, що
за умови, що ![]() а
а ![]() — правильна. Область
— правильна. Область ![]() вважатимемо правильною, якщо прямі,
паралельні координатним осям, перетинають її границю не
більше, ніж у двох точках. Нехай границя області D
записана рівняннями
вважатимемо правильною, якщо прямі,
паралельні координатним осям, перетинають її границю не
більше, ніж у двох точках. Нехай границя області D
записана рівняннями ![]() (ближня до осі ОХ її частина) і
(ближня до осі ОХ її частина) і
![]() (віддалена частина). Схема міркувань така.
З одного боку,
(віддалена частина). Схема міркувань така.
З одного боку,![]() де
де ![]() — об'єм
відповідного циліндричного тіла, а з другого боку, подавши
— об'єм
відповідного циліндричного тіла, а з другого боку, подавши ![]() відповідним чином, матимемо спосіб
обчислення
відповідним чином, матимемо спосіб
обчислення ![]() .
.
Для цього
застосуємо формули площі криволінійної трапеції та об'єму тіла з відомими
поперечними перерізами, тобто 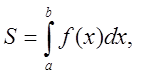
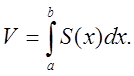 (пригадаймо матеріал ІІ-го семестру)
(пригадаймо матеріал ІІ-го семестру)
Площа
поперечного перерізу циліндричного тіла площиною, паралельною ![]()
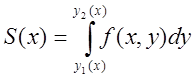 ( на
рис. 4.2 такий переріз заштриховано).
( на
рис. 4.2 такий переріз заштриховано).
Шуканий об'єм має вигляд 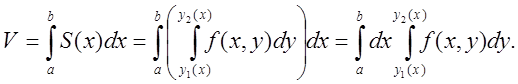 (4.5)
(4.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.