Подвійні інтеграли. Задачі, що приводять до поняття подвійного інтнграла. Означення і властивості подвійного інтегралу, страница 5

Тому ми можемо сказати, що відрізки  мають однакову довжину і однаково направлені. Те ж саме можна сказати і про відрізки , тобто фігура  є паралелограм і його площу можна знайти як модуль векторного добутку векторів-сторін ,тобто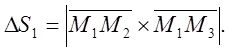  

Обчислимо координати векторів-множників.

 

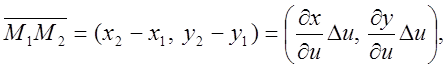
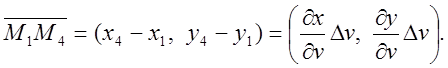
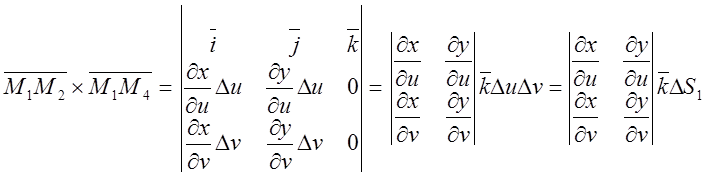   , враховуючи, що  одержимо 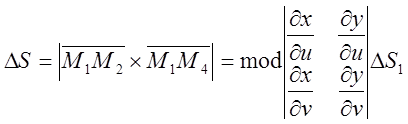    Звідси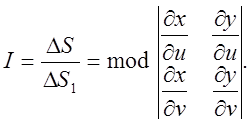 

Цей функціональний визначник називають визначником Якобі чи якобіаном. Формулу (4.8) дістав М.В.Остроградський. При заміні змінних з n числом координат (наприклад у трьохвимірному просторі) якобіан переходу дорівнюватиме модулю визначника n-го порядку  (в трьохвимірному просторі – третього).

При переході до полярної системи координат  як наслідок вище сказаного     маємо 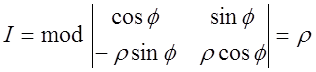  . Тоді

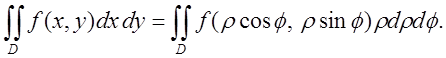                                                        (4.9)

Формула (4.9) є формулою переходу в подвійному інтегралі від прямокутних декартових координат до полярних.

                                                       4.5. Приклади

П.2.Обчислити повторний інтеграл

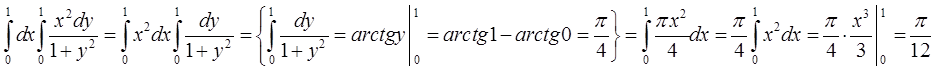Відповідь:

П.3.Розставити границі інтегрування в тому і в другому порядку в подвійному інтегралі

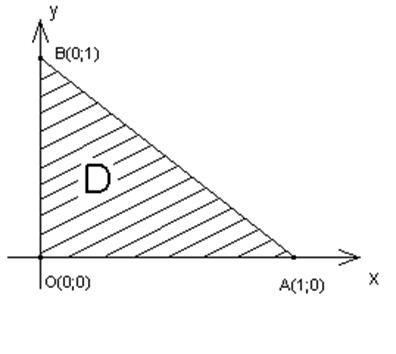
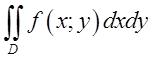, де - трикутник з вершинами .(рис.1).

 Розв’язок: побудуємо область. Запишемо рівняння ліній, які обмежують область: це осі. Рівняння прямої  будемо шукати у вигляді: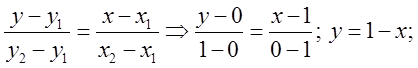

Розпишемо подвійний інтеграл через    повторний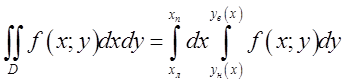;де   Рис.4.5.

;- (індекси внизу ікса - означають крайня ліва  і крайня права координата області по змінній х)   визначити дуже легко; - це значення змінної , яке приймає поточна (текущая) точка, знаходячись в крайній лівій частині області . Аналогічно - це значення змінної , яке приймає поточна точка знаходячись в крайній правій частині області . В нашому випадку . Значення  і - (нижнє і верхнє) знайти важче, бо вони будуть залежати від тих значень змінної , які вона приймає в межах попереднього інтегрування. Обчислимо їх декілька, використовуючи рівняння границь області і застосовуючи рисунок 1. 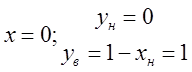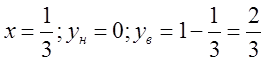При ;  при ;   при ;     ми знаходимо, підставляючи  в рівняння, яке обмежує область  знизу;  ми знаходимо, підставляючи  в рівняння, яке обмежує область  згори. А тому в загальному випадку в другому інтегралі границями повинні стояти функції і ; Відповідь:.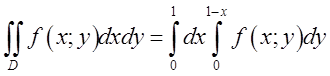

П.4. Перемінити порядок інтегрування в повторному інтегралі

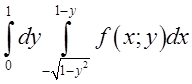
Розв’язок: випишемо рівняння ліній, які обмежують область    інтегрування : , або  при   , або . Зобразимо область (рис.4.6). Областю буде криволінійний трикутник . Якщо змінна  буде змінюватись від  до  то змінна величина  буде змінюватись від  в точці до 0 в точці. , за величиною буде дорівнювати висоті стовпчика, яка буде залежати від того значення  в якому знаходиться точка.Очевидно, що для інтервалу зміни  від  до  значення  буде увесь час

                   Рис 4.6.

дорівнювати. В цей час  буде зростати від до , причому, це зростання йтиме вздовж дуги кола , або . Так буде до тих пір доки точка  не дійде до. (В цей час точкадійде до точки ). В точці  порушується умова гладкості кривої, бо в ній невизначена похідна . В точці  точка  переходить з кривої  на лінію . З цієї причини ми вимушені, користуючись властивістю адитивності подвійного інтеграла , розбити його на два інтеграли: один по області, четвертина кола ; другий по області ; частина площини першого квадрату обмежена трикутником . 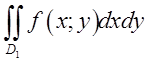В інтегралі по області     змінюється від до  в зовнішньому інтегралі і  змінюватиметься від  до  у внутрішньому, тобто :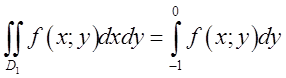. Для кращого розуміння розстановки границь можна, як до прикладу технічної реалізації ідеї, звернутись до роботи телевізора. Якщо горизонтально відхиляюча система електроніки промінь буде відхиляти від точки  до точки , то щоб одержати на екрані зображення сектора , треба у вертикальному напрямку промінь ганяти від прямої  до кривої . Якщо протягом одного відхилення по горизонталі буде виконуватись декілька сот відхилень по вертикалі, то рисочки  зільються і ми одержимо зображення сектора. Аналогічно, 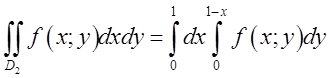. Відповідь: 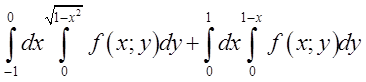. Коли виникає потреба змінювати порядок інтегрування? Коли має ця операція сенс в вище наведеному прикладі, особливо якщо врахувати, що у відповіді одержали суму двох інтегралів. Очевидно переміна місць інтегрування вигідна тоді коли  обчислюється набагато простіше ніж. Інколи переміна місць дає виграш і в обчисленні інтеграла і спрощує сам інтеграл (замість декількох, виходить один).