Подвійні інтеграли. Задачі, що приводять до поняття подвійного інтнграла. Означення і властивості подвійного інтегралу, страница 4

                         Міркуючи аналогічно, в результаті перетину циліндричного тіла паралельними

площинами, .            XOZ, маємо V=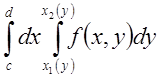      (4.6)

 

 Оскільки І = V, то, враховуючи (4.5) і (4.6), знаходимо

              Рис.4.2

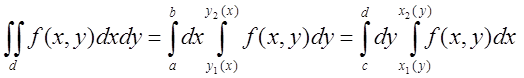                                                  (4.7)        

або схематично (1) = (2) = (3).       

 Конструкції (2) і (3) називають повторними інтегралами. Розрізняють зовнішній і внутрішній інтеґрали. Перехід (1) = (2) чи (1) = (3) означає обчислення інтеґрала, а перехід від (2) до (3) чи навпаки – зміну порядку інтеґрування. Така зміна, крім (4,7), забезпечується також конструкцією (4.4а), в якій ми можемо змінити індекси при обчисленні суми.  Зазначимо, що (4.7) справджується в будь-якому випадку, а не тільки для (х, у)  0. Для конструкції (4.4а) знак функції f(x,y) не відіграє ніякої ролі. У разі неправильної області для обчислення відповідного інтеґрала користуються властивістю 2, п. 4.2., розбиваючи її на декілька правильних областей.

 П.1. Обчислити 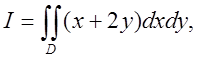 область D обмежена лініями у = 0, у = х, х + у = 2.

Зображуємо область D (рис. 4.3). Якщо зовнішній інтеґрал береться по змінній х, то очевидно, що в нього границі інтегрування будуть . Під час зміни х від 0 до 1, у внутрішньому інтегралі у буде змінюватись від прямої у=0 до прямої у=х. Але якщо х буде змінюватись далі від 1 до 2, то верхня границя зміни у стане іншою, а саме . В                        Рис.4.3                       точці (1,1) верхня границя внутрішнього інтегралу “ламається” – з одної лінії переходить на іншу, а тому ми розбиваємо прямою х=1 область інтегрування на дві області і одержимо відповідно з 4.2.2 суму двох інтегралів 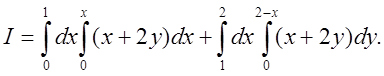 Щоб знайти відповідь треба обчислити чотири інтеграли.

Якщо ж зовнішній інтеграл візьмемо за змінною у, то очевидно, що . Пряма, паралельна осі ОХ якщо її рухати від положення у=0 до положення у=1, входитиме в область на прямій х=у, а виходитиме з неї на прямій х=2-у. А тому маємо 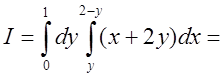 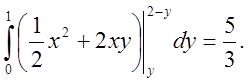Вибір напряму інтеґрування в    подвійному інтегралі, як бачимо, може мати значення для  зменшення обсягу обчислень.

4.4. Заміна змінних у подвійному інтегралі

 Нагадаємо схему заміни змінних у визначеному інтеґралі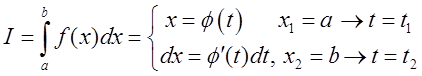 

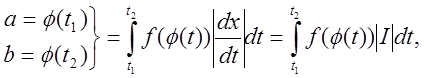
де  — відношення довжин елементарних частин при старій та новій змінних. Нехай маємо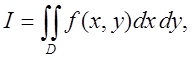

                                   

                    а)                             Рис 4.4                          б)

а заміну здійснюємо за допомогою формул  причому, за аналогією з одновимірним інтегралом 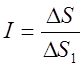 — відношення площ елементарних частин при , старих і нових змінних (рис. 4.4, а). Природньо вважати, що тоді

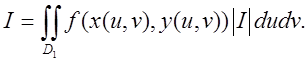                                                                   (4.8)

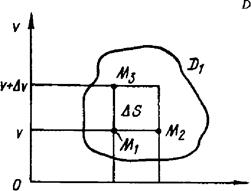
У випадку нових змінних  Щоб знайти площу елементарної частинки  при старих змінних (рис. 4.4, б), зазначимо, що при відображенні області  на (на рис. 4.4.б зображена її деяка частина) за допомогою  елементарний прямокутник  переходить в елементарний паралелограм (нижче ми це доведемо) .

 Зауважимо, що точки  лежать на лінії . Аналогічно точки  лежать на лінії . Точно так же точки  лежать на лінії , а точки  лежать на лінії .   Знайдемо координати цих точок  виражені через нові змінні u i v.

Для точки  маємо

 Користуючись формулою Тейлора для двох змінних (пригадаємо її: ),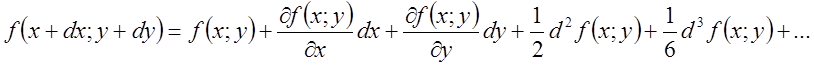

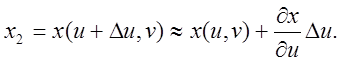для точки  знаходимо    Знак  стоїть тому, що ми обмежились в формулі Тейлора лише двома членами, вважаючи другий і всі вищі диференціали величинами вищого порядку малості в порівнянні з першим диференціалом. Крім того, завдяки тому, що   лежать на лінії , .

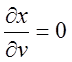Аналогічно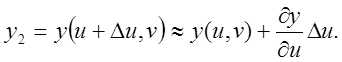     

 Для точки  маємо: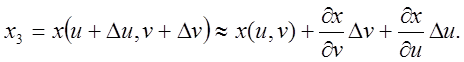      

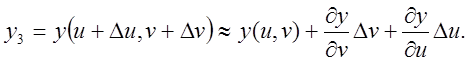
Для точки маємо: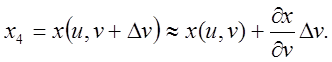     

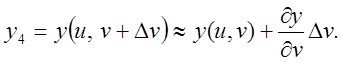
Із знайдених виразів витікає, що (перевірте) , а також  .