Подвійні інтеграли. Задачі, що приводять до поняття подвійного інтнграла. Означення і властивості подвійного інтегралу, страница 2

3. Іноді область задається нерівністю, наприклад . Щоб уникнути помилки треба міркувати так: крива  розбиває область, якою є вся площина хОу на дві області: зовні кола і всередині кола. Якщо ми візьмемо точку знаючи, що вона знаходиться зовні кола, наприклад  і зясуємо, що вона не належить до області, то і всі інші точки, які лежать зовні також не належать до області. Звідси висновок: область утворюють точки, які лежать всередині кола і на його границі, бо нерівність нестрога. А зясувати належить точка до області чи не належить дуже просто – досить підставити координати вибраної точки в нерівність. Якщо нерівність справджується, то точка  належить області, а якщо не справджується – то не належить.

            Не обовязково, щоб крива була замкнута (коло, еліпс і т. ін.), пряма, парабола, гіпербола та інші незамкнуті криві також ділять область хОу на дві підобласті, границею між якими вони являються. І до них правомірні ті ж міркування, що й до замкнутих кривих. Коли область задано як перетин множин розвязків декількох нерівностей то й знаходять цей перетин, методом штриховки областей, наприклад, якщо область задано 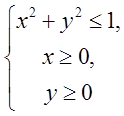  то заштрихувавши  одиничний  круг, праву напівплощину і верхню напівплощину – побачимо, що перетином множин всіх трьох розвязків є четверта частина одиничного круга, розміщена  в першому квадранті.

4.Треба пригадати таблицю інтегрування: 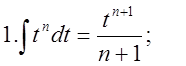2.    

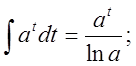
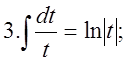
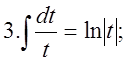
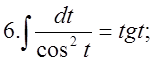
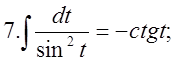
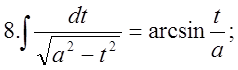
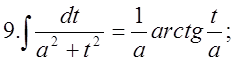
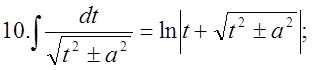
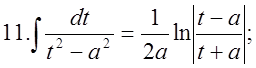
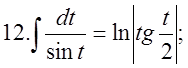
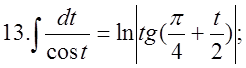
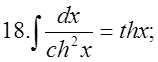
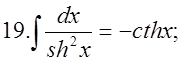
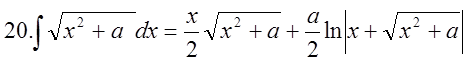
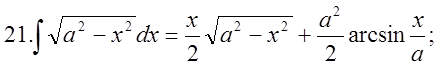
4.1. Задачі, що приводять до поняття подвійного інтеграла

Задача про  об’єм  циліндричного тіла

 О. Циліндричним називається тіло, обмежене деякою поверхнею, проекцією її на координатну площину і циліндричною поверхнею, для якої контур вказаної проекції є напрямною.

 О. Діаметром області називається найбільша з відстаней між двома довільними точками цієї області.

 Позначимо діаметр області D через .

 Знайдемо об'єм циліндричного тіла, обмеженого поверхнею , проекцією D  поверхні на площину ХОУ, відповідною циліндричною поверхнею за умови, що  неперервна і невід'ємна в D.

 Розв'язування задачі аналогічне розв'язуванню задачі про площу кри­волінійної трапеції. Розіб'ємо довільним способом D на п частин  і відповідним чином весь об'єм на суму п елементарних об'ємів (рис. 4.1). Нехай , — множина точок відповідної і-ї частини D і площа цієї частини. Зробимо істотне припущення – висота кожного “елементарного паралелепіпеда” постійна (хоч насправді вона є функцією від х,у) тобто: ,                                 (4.1)

За такої умови об'єм і-ї елементарної частини циліндричного тіла

  Тоді             ;

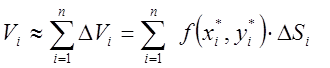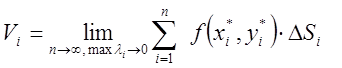                                       (4.2)

         Рис. 4.1                         де ­– діаметр , якщо така границя існує.

                   Задача про масу плоскої пластинки.

 Нехай плоска пластинка займає область D, а густина пластинки визначається неперервною функцією . Знайти масу т пластинки.

 Розбивши область D на частини, як в першій задачі і зробивши припущення, як в (4.1), матимемо 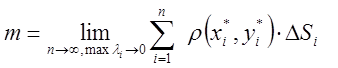                                                (4.3)

4.2. Означення і властивості подвійного інтеграла

З математичної точки зору розв'язки (4.2) і (4.3) мають однаковий вигляд. Отже, є сенс вивчати конструкції такого типу. За аналогією з вивченими раніше одновимірними інтегралами ці границі сум називатимемо  подвійними інтеґралами. Скористаємося деякими позначеннями з попередніх задач.

О. Подвійним інтегралом від функції  по області D називається границя

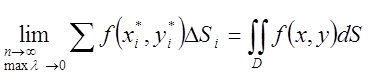                                                                  (4.4)