4.Перемінити
порядок інтегрування 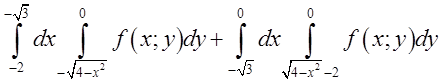
 Розв’язок: маємо
Розв’язок: маємо 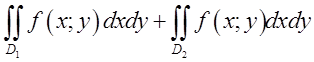 .Область
.Область ![]() обмежена лініями
обмежена лініями ![]() або
або 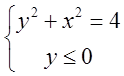 ;
; ![]() ; Область
; Область ![]() обмежена лініями
обмежена лініями ![]() або
або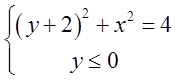 ;
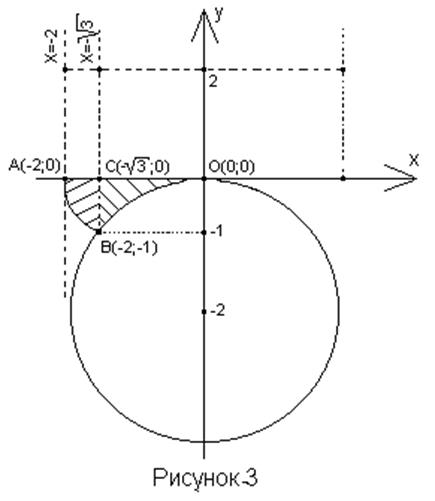
; ![]() ; Побудуємо обидві області
на рисунку 3.
; Побудуємо обидві області
на рисунку 3. ![]() - це область,
обмежена криволінійним трикутником
- це область,
обмежена криволінійним трикутником ![]() .
. ![]() - це область,
обмежена криволінійним трикутником
- це область,
обмежена криволінійним трикутником ![]() . Як бачимо області
. Як бачимо області ![]() .
.
Найближче в області ![]() лежить
точка
лежить
точка ![]() .
. ![]() ; найвище лежать точки, які
розташовані на прямій
; найвище лежать точки, які
розташовані на прямій ![]() . Тому в
першому інтегралі
. Тому в
першому інтегралі ![]() .
.
В цей час коли так змінюється ![]() в другому інтегралі
в другому інтегралі ![]() буде
“бігати” по кривій
буде
“бігати” по кривій ![]() від
точки
від
точки ![]() до точки
до точки ![]() . Запишемо рівняння кривої в
явній формі
. Запишемо рівняння кривої в
явній формі ![]()
![]() так як
так як ![]() ,
, ![]() , то
, то ![]() або остаточно
або остаточно ![]() .
.
Рис.4.7.
Правою границею для ![]() буде
крива
буде
крива ![]() від точки
від точки ![]() до точки
до точки ![]() .Виразимо цю криву також в
явній формі
.Виразимо цю криву також в
явній формі ![]() ;
; ![]() ,
, 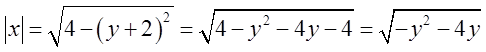 .
.
На ділянці ![]()
![]() ; тому
; тому ![]() ; остаточно маємо:
; остаточно маємо: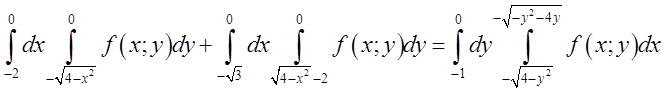 .
.
 П.5. Обчислити
П.5. Обчислити 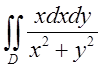 , де
, де ![]() - параболічний сегмент, обмежений
параболою
- параболічний сегмент, обмежений
параболою 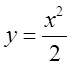 і прямою
і прямою ![]() .
.
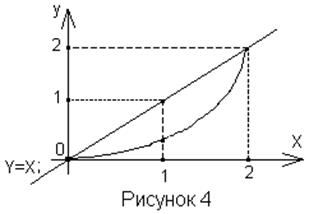
Розв’язок: побудуємо область![]() . Парабола
. Парабола 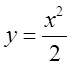 перетне пряму
перетне пряму ![]() в двох точках з
в двох точках з
координатами (0,0)
і (2,2). А тому ![]() а у в
а у в
Рис.4.8.
цей час буде
змінюватись в межах від 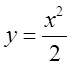 до
до ![]() .
.
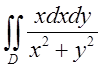 =
=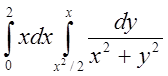 =
=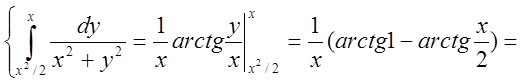
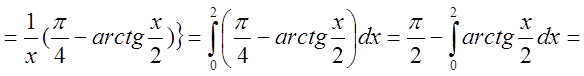
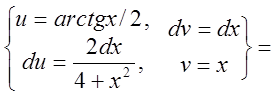
=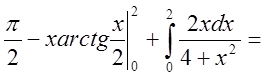
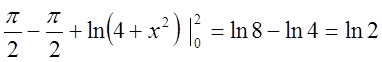 .
.
Відповідь:![]()
П.6. Обчислити
інтеґрал Ейлера-Пуассона![]()
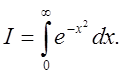
Розв'язання . Оскільки 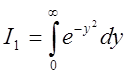 відрізняється від І лише формою запису змінної (замість х
стоїть у) то їх величини будуть однакові, а тому
відрізняється від І лише формою запису змінної (замість х
стоїть у) то їх величини будуть однакові, а тому ![]() . Крім того
. Крім того ![]() . А
тому
. А
тому 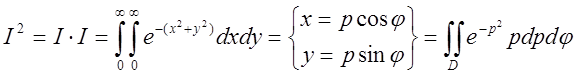
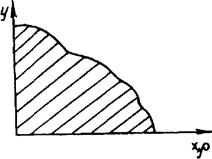 Обчислимо останній інтеґрал (рис. 4.9). Областю інтегрування є перший октант
Обчислимо останній інтеґрал (рис. 4.9). Областю інтегрування є перший октант ![]() . В полярній системі цю
область утворить промінь, який буде виходити з полюса, а тому
. В полярній системі цю
область утворить промінь, який буде виходити з полюса, а тому ![]() , і прямуватиме в нескінченність, а тому
, і прямуватиме в нескінченність, а тому ![]() . Це будуть межі внутрішнього інтегралу по
. Це будуть межі внутрішнього інтегралу по ![]() . Починати свій рух промінь повинен з
положення
. Починати свій рух промінь повинен з
положення ![]() , а тому це буде нижня границя зовнішнього
, а тому це буде нижня границя зовнішнього
Рис. 4.9 інтегралу по ![]() , а закінчити свій рух промінь має в
положенні
, а закінчити свій рух промінь має в
положенні 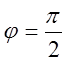 , і це буде верхня границя зовнішнього
інтегралу. Маємо
, і це буде верхня границя зовнішнього
інтегралу. Маємо 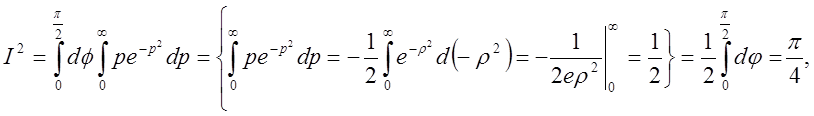 звідки
звідки 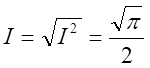 тобто
тобто 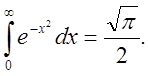 (4.10)
(4.10)
Цей інтеґрал широко застосовується в теорії ймовірностей.
Запитання для самоперевірки.
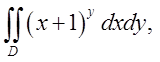 де область D квадрат
де область D квадрат ![]() .
.
Розвяжіть самостійно.
1.1. 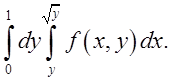 Відп.
Відп.
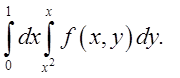
1.2. 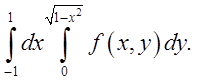 Відп.
Відп.
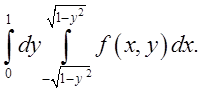
1.3.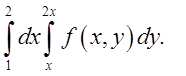 Відп.
Відп. 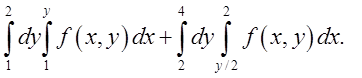
1.4.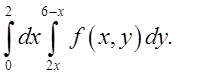 Відп.
Відп.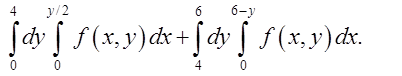
2.1. Відп.
Відп. ![]()
2.2.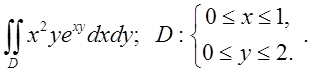 Відп. 2.
Відп. 2.
2.3.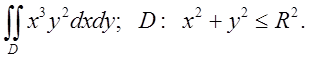 Відп. 0.
Відп. 0.
2.4.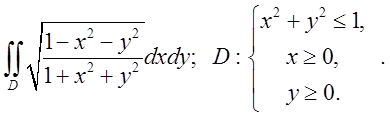 Відп.
Відп.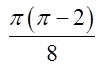 .
.
2.5.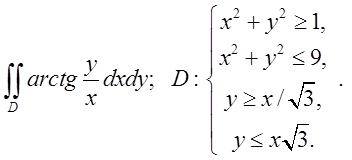 Відп.
Відп.![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.