Информатика и выч. техника \ Моделирование

Проектирование цифрового автомата в САПР OrCAD 9.1 и Active-HDL 8.1, страница 7

              K0<=not J0                                                      after 12ns;

              K1<=not J1                                                       after 12ns;

              K2<=not J2                                                       after 12ns;

              K3<=not J3                                                       after 12ns;

              process(C,R) 

              begin    

              if(R='0') then QP <= (others => '0') after 25ns;

              elsif(C='1' and C'EVENT) then     

              QP(0)<=(not(K0) and QP(0)'DELAYED)or (J0 and not(QP(0)'DELAYED)) after 24ns;

              QP(1)<=(not(K1) and QP(1)'DELAYED)or (J1 and not(QP(1)'DELAYED)) after 24ns;

              QP(2)<=(not(K2) and QP(2)'DELAYED)or (J2 and not(QP(2)'DELAYED)) after 24ns;

              QP(3)<=(not(K3) and QP(3)'DELAYED)or (J3 and not(QP(3)'DELAYED)) after 24ns;    

              end if;

              end process;

Q<=QP;

end \M14-DR_POT\;

Как видно из текста в потоковой модели неявно присутствуют все элементы схемы замещения.

В потоковой модели было использовано характеристическое уравнения JK-триггера:

Q(t+1)=J*not(Q(t) \/ not(K)*Q(t);

На рисунке 4 представлены все сигналы, которые используются в потоковой модели – это нужно для наглядности и понимания потоковой  VHDL-модели.

Результаты верификации потоковой VHDL-модели представлены на рисунке 11.

Как видно из временной диаграмм на рисунке 11.1 задержки совпадают с задержками, полученными на зарубежных символах (рис. 5 и 5.1).


Рис. 10 Результаты верификации функциональной модели ЦА

Рис. 11 Результаты верификации потоковой модели ЦА

                                                                                                                              

             

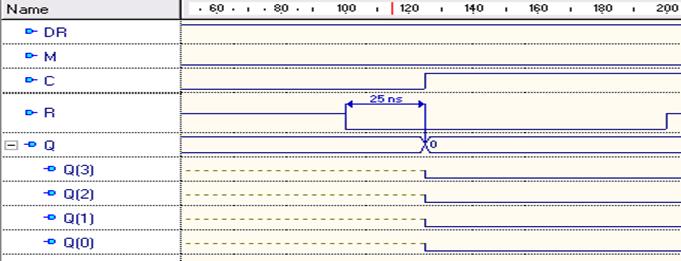
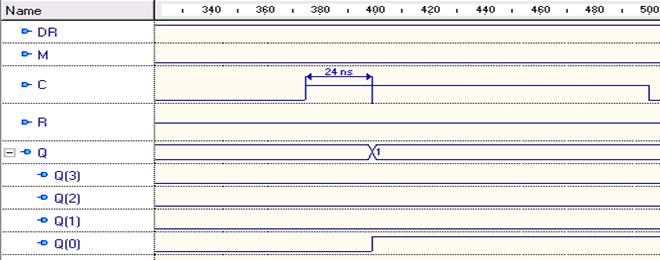
Рис. 11.1 Результаты верификации потоковой модели ЦА (отображено время задержки по сбросу R и по фронту С)

Синтез комбинационной части автомата на мультиплексорах с использованием разложения Шеннона

Для начала некоторая теоретическая информация.

Универсальные логические модули (УЛМ) на основе мультиплексоров отно­сятся к устройствам, настраиваемым на решение той или иной задачи. Уни­версальность их состоит в том, что для заданного числа аргументов можно настроить УЛМ на любую функцию. Известно, что общее число функций n аргументов выражается как 2^2n  Сростом n число функций растет чрезвычайно быстро. Возможность получить любую из огромного числа функций свидетельствует о больших перспективах применения УЛМ.

Первая теорема Шеннона: Любая булева функция f(x1,x2,…,xn) представима в виде разложения Шеннона:

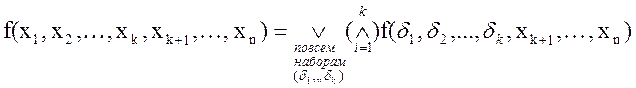
Большое число входов настройки можно уменьшить, расширив алфавит настроечных сигналов. Если от алфавита {0, 1} перейти к алфавиту {}, - литера(либо сама переменная, либо её инверсия) одного из аргументов, то число входов аргументов сократится на единицу, а число настоечных входов – вдвое.

Для нового алфавита код настройки находится следующим образом. Аргументы за исключением  подаются на адресующие входы, что соответствует их фиксации в выражении для искомой функции, которая становится функцией единственного аргумента . Эту функцию, которая называется остаточной, и нужно подавать на настроечные входы.

В настроечные сигналы следует переводить аргумент, который имеет минимальное число вхождений в термы функции. В этом случае будут максимально использованы как бы внутренние логические ресурсы мультиплексора, а среди сигналов настройки увеличится число констант, что и считается благоприятным для схемной реализации УЛМ.

В примере для функции возбуждения J0(M, Q3, Q2, Q1, Q0) наименьшее число вхождений имеет аргумент Q2, поэтому мы его переводим в настроечные сигналы, а на адресные входы мультиплексора соответственно будем подавать  

Скачать файл