Методологические основы предмета «Теория систем и системный анализ». Инструментарий системного анализа. Моделирование в системном анализе. Критерии системного анализа. Неопределенность в системном анализе, страница 14

Принимая решение, необходимо учитывать все обстоятельства, которые могут повлиять на результаты этих решений. Однако часть условий, касающихся будущего развития системы не всегда удается предугадать, т.е. для большинства решений по сложным проблемам характерным является наличие неопределенности, под которой нужно понимать процессы и явления, исходы которых нельзя предсказать или спрогнозировать. 

В системном анализе учитывается 2 рода неопределенностей:

- неопределенность первого рода: обуславливается внутренними свойствами объектов, является следствием изменений в объекте, которые еще не учтены в модели. Параметры таких явлений характеризуются случайностью своих проявлений. Такие факторы встречаются при исследовании массовых, повторяющихся явлений. Ситуации, в которых возникают неопределенности этого типа называются ситуациями риска. Они характеризуют ситуации, когда каждая возможная альтернатива известна, известно полное множество исходов и вероятность каждого исхода. Неопределенность заключается в том, что неизвестно к какому именно исходу приведет реализация данной альтернативы. Задачи решаются методами теории вероятностей;

Согласно аксиомам теории вероятностей всякому случайному событию А может быть поставлено в соответствие вещественное число Р(А) – вероятность события А, находящееся между нулем и единицей.

При этом вероятность наступления одного из двух несовместимых (т.е. взаимоисключающих) событий равна сумме их вероятностей

Р(А или В) = Р(А) + Р(В)

Вероятность совместного осуществления двух независимых событий равна произведению их вероятностей          

Р(А и В) = Р(А) · Р(В)

Если событие А может осуществиться лишь при условии, что происходит одно из несовместных событий В₁, В₂, …, В_n, вероятности которых известны, то полная вероятность этого события А будет равна

Р(А) = 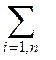Р(В_i) · Р(А/В_i)

Если некоторое событие В вызывается действием какой-либо из m причин А₁, А₂, …, А_m, то вероятность того, что событие В было вызвано причиной А₁ или А₂ или …, А_m , равна

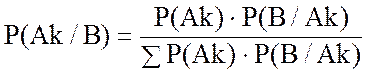
Эта формула, известная под названием теоремы Байеса, имеет много практических применений, в том числе и в теории решений и в системном анализе.

- неопределенность второго рода: связана с неполнотой сведений об объекте и условиях функционирования. Возникают, когда неизвестно, какой из законов случайных событий действует в данном конкретном случае, т.е. альтернативы и исходы известны, но неизвестны вероятности исходов или они лишены смысла. Для решения этих задач используется аппарат теории игр, в частности теории стратегических и статистических решений.

Основанием для выбора стратегий в подобной ситуации может быть максимизация ожидаемой чистой выгоды, представляющего собой средневзвешенную сумму прибылей, которую могут дать все исходы по данной стратегии, причем весом каждого исхода будет вероятность его реализации, то есть

H_i = h_ij · p_j , где h_ij - выигрыш, получаемый игроком при выборе i–ой стратегии при реализации j–ого состояния природы;  

p_j – вероятность  реализации j–ого состояния природы.

Здесь под природой понимается вся совокупность внешних обстоятельств, развивающихся и действующих в соответствии со своими законами и оказывающих влияние на результаты принимаемых решений.

Данное соотношение выражает основную идею теории статистических решений, однако такой простой принцип может быть использован при выработке решения только в простейших случаях.

В других,  более сложных ситуациях можно предложить другие принципы выбора в условиях неопределенности, как принцип «максимина», критерии Вальда, Гурвица, Сэвиджа, Байеса-Лапласа и другие, которые  могут быть применены как при наличии, так и при отсутствии информации об оценках вероятного состояния природы.

Если ситуация, в которой принимается решение, представлена не только неопределенными условиями внешних обстоятельств, но включают также и действия разумных существ, чью деятельность принимающий решение не может контролировать, то для решения задачи применяется аппарат теории стратегических игр.