Компоновка сечений ветвей выполняется при их рассмотрении аналогично поясам вертикальной фермы. Эта аналогия обусловлена и характером их нагружения – усилиями осевого сжатия, и характером их деформирования в предельном состоянии – между условно шарнирными узлами закреплений (в плоскости рамы – узлами крепления элементов нижних связей колонн), и, как следствие, порядком определения расчетных длин, при m=1, когда lox=d; loy=h. Для определения усилий в ветвях необходимо применить разложение комбинации усилий в сечении колонны, например, как это показано на рис.39а для подкрановой ветви. В соответствии с ним имеем:
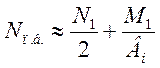
где знаки N1 и M1 уже учтены. Приближенность этого разложения очевидна. Во-первых, центр тяжести сечения колонны помещен в середину ‘‘Вн’’; во-вторых, расстояние между центрами тяжести ветвей принято равным ‘‘Вн’’ (оба допущения грубы и приемлемы лишь как вспомогательные на начальном этапе). В шатровой ветви найдем по аналогии
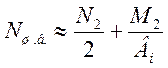
Имея для ветвей усилия и расчетные длины, можно подобрать их сечения, как сечения центрально-сжатых сплошных стержней швеллерного и двутаврового вида, исходя из рекомендуемой по (1, п.5.6) гибкости lх=80 и по опыту - lу=80…90. Каждое из скомпонованных сечений должно быть проверено на общую устойчивость для чего определяются – Ав, Jx (попутно для шаровой швеллерной ветви у1 – привязка ее центра тяжести по рис. 39б), Jy, ix, iy, lх, lу (обе …£80), а в итоге - lмах, jmin и
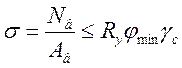
Выполнение этого условия может потребовать корректировок сечений ветвей, после чего следует уточнить положение центра тяжести всего сечения колонны, определив его привязки у2 и у3 по рис. 39б. Если окажется, что у3=Вн/2, то переходить к следующему пункту. Если у3¹Вн/2, т.е. положение центра тяжести уточнится, то необходимо уточнить и усилия в ветвях
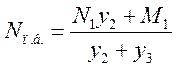
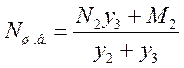
а затем проверить их общую устойчивость опять же с возможной корректировкой (но теперь незначительной) сечений. Процедура уточнения усилий и сечений-затухающая, в один – два цикла.
Подбор сечений элементов решетки естественно с уточнения расчетного усилия, которое зависит от поперечной силы в сечении колонны и обжатия ее ветвей. На основании статических расчетов мы уже имеем Qfac=|Qmax|. С учетом гибкости колонны и характера ее предельного состояния можно найти и условную поперечную силу по (1, п. 5.8) или по (2, табл. 8.2), что более определено, как
Qfic=к (Аш.в.+Ап.в.)
где к=0,2 кН/см2 – для сталей марки Вст3,
к=0,3 кН/см2 – для сталей марки 14Г2, 15ХСНД
к=0,4 кН/см2 – для сталей марки 10ХСНД.
По найденным Qfac и Qfic расчетная поперечная сила Qmax принимается как большая. Тогда из условия равновесия получим
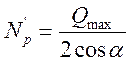
где двойка указывает число плоскостей решеток. Усилие Np’’, связанное с упругим обжатием ветвей, найдем рассмотрев схему по рис.40. В качестве расчетной рассматривается наиболее напряженная ветвь, с большим отношением Nв/Ав (в нашем случае – подкрановая). Укорочение полупанели ветви составит
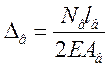
При этом укорочение раскоса можно найти аналогично
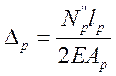
или геометрически
![]()
Указывая на эти выражения, найдем
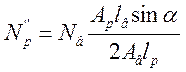
и в целом
![]()
В полнее очевидно, что искомое усилие зависит от сечения раскосов, т.е необходимо задать им (обычно в пределах L50X5…L125X10) найти Np и оценить его общую устойчивость, как обычно центрально-сжатого стержня, по формуле
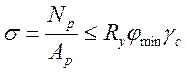
с последующей корректировкой при необходимости.
Особенности здесь следующие:
- во-первых, раскос по характеру работы аналогичен промежуточному раскосу фермы, поэтому lор=0,8 lр;
- во-вторых, в сечении колонны находятся два раскоса, сам же раскос – одиночный уголок, поэтому i=ix или iy (что меньше, если уголок неравнополочный) (1, п.6.4), а gс=0,75 (1, табл. 6, поз. 9б).
Проверка общей устойчивости колонны в плоскости рамы (из плоскости ветви и, следовательно, вся колонна проверены в первом пункте) выполняется момент инерции подобранного сечения – Jx, напомним (см. рис. 39б),
![]() ,
,
собственными моментами инерции ветвей здесь можно пренебречь ввиду их сравнительной малости. Для комбинации расчетных усилий с большей N находим эксцентриситет приложения силы
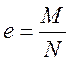
и относительный эксцентриситет
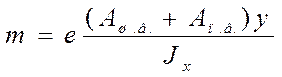 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.