Это происходит потому, что при замыкании цепи течет кратковременный ток зарядки конденсатора. После того как конденсатор зарядился, ток в цепи прекращается. Если подобную цепь (но с амперметром переменного тока) подключить к источнику переменного тока, можно заметить, что в цепи непрерывно протекает ток, На первый взгляд, это кажется удивительным: в цепи, разомкнутой диэлектриком конденсатора, протекает ток, Однако в этом нет ничего удивительного. Конденсатор в течение первой четверти периода заряжается, на его пластинах появляются электрические заряды. В течение второй четверти периода конденсатор разряжается, возвращая энергию источнику. Затем в течение третьей четверти конденсатор вновь заряжается, а в течение четвертой четверти он разряжается. В цепи течет ток перезарядки конденсатора, который представляет собой вынужденные электрические колебания. Присоединим к лабораторному генератору переменного тока лампочку накаливания. Лампочка ярко светит рисунок 23 , мы заметим, что лампочка стала светить менее ярко. Это свидетельствует об уменьшении силы тока в цепи, что может быть объяснено увеличением сопротивления. Следовательно, конденсатор оказывает переменному току некоторое сопротивление, которое получило название емкостного сопротивления; его обозначают через Хс.
б) Фазовые соотношения. Подключив двух лучевой осциллограф к клеммам
конденсатора С и активного сопротивления R, заметим, что
осциллограмма напряжения, снимаемая с конденсатора, не совпадают по фазе рисунок
25. Внимательный анализ осциллограмм показывает, что колебания тока и
колебания напряжения в цепи с конденсатором сдвинуты по фазе на 
. При этом колебания
тока опережают по фазе колебания напряжения.
Первоначально это кажется необычным. Однако результаты опыта имеют простой физический смысл. Напряжение на конденсаторе определяется имеющимся на нем электрическим зарядом. Но этот заряд образован током, протекавшим в более ранней стадии колебательного процесса. Поэтому колебания напряжения запаздывают относительно колебаний силы тока.
в) Закон Ома. Несовпадение колебаний силы тока и напряжения по фазе приводит к тому, что закон Ома (в том виде, в каком он сформулирован для постоянного тока) в цепи переменного тока с конденсатором несправедлив для мгновенных значений тока и напряжения. Но он, однако, справедлив для действующих значений, в этом можно убедиться на опыте. Меняя напряжение, мы увидим, что сила тока в цепи пропорциональна напряжению:
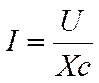
где Хс – емкостное сопротивление конденсатора. Понятно, что такое же соотношение существует между амплитудными значениями силы тока и напряжения:
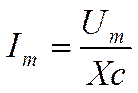
г) Формула емкостного сопротивления. Выясним, от чего и как зависит емкостное сопротивление. Для этого вспомним, что в любой момент времени напряжения на конденсаторе определяется формулой
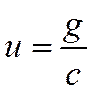
где заряд g на обкладках конденсатора изменяется по гармоническому закону:
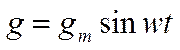
известно, что
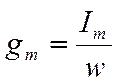
Поэтому:
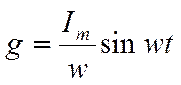
Подставив значение заряда в формулу напряжения, получаем:
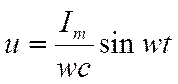
Напряжение будет максимальным при wt= 1. Следовательно,
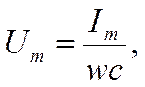
откуда:
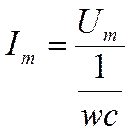
Так
как закон Ома справедлив для максимальных значений тока и напряжения, то
величина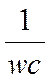 
имеет смысл емкостного сопротивления:
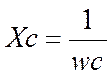
Заменив циклическую частоту на её выражение через частоту колебаний, получим:
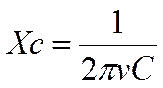
Определим, например, емкостное сопротивление конденсатора емкостью 130мкФ при частоте тока 50Гц:
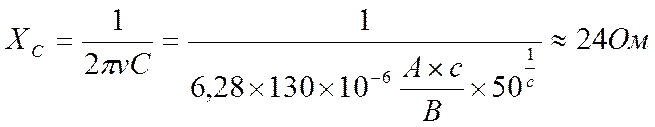
д) Преобразование энергии. Найдем мощность в цепи переменного тока, содержащей только конденсатор. Мы знаем, что мощность в цепи переменного тока можно подсчитать по формуле
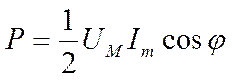
Преобразуем эту формулу так, чтобы можно было заменить максимальные значения тока и напряжения через их действующее значение:
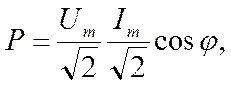
или
Так как сдвиг по фазе между колебаниями тока и напряжения при емкостной нагрузке равен
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.