При торможении точки подвеса рисунок 55 б g′3 = g + а3, где а3 = а1, так как точка подвеса тормозится до остановки столько же времени, сколько разгоняется из состояния покоя (по условию t1 = t3 = 3, 0 с). При движении в горизонтальном направлении (рис. 55, в)
g′4
= 
= 
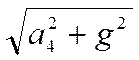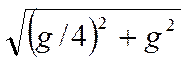
Определяем периоды колебаний маятника на каждом участке пути:
Т1 = 2π
= 2π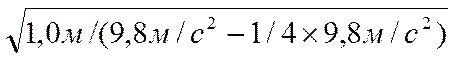
≈ 2,3 с,
__ _____________
Т2 = 2π√ l/g = 2π√ 1,0 м / 9, 8 м/с2 ≈ 2,3 с,
Т3 = 2π√ l/(g + а1) = 2π√ 1,0 м / (9,8 /с2 + ¼ 9,8 м/с2) ≈ 1,8 с,
Т4 = 2π√ l
Ответ: Период колебаний маятника на первом участке пути Т1 ≈ 2,3 с; на втором участке Т2 ≈ 2,0 с; на третьем участке Т3 ≈ 1,8 с; при горизонтальном движении Т4 ≈ 0,62 с.
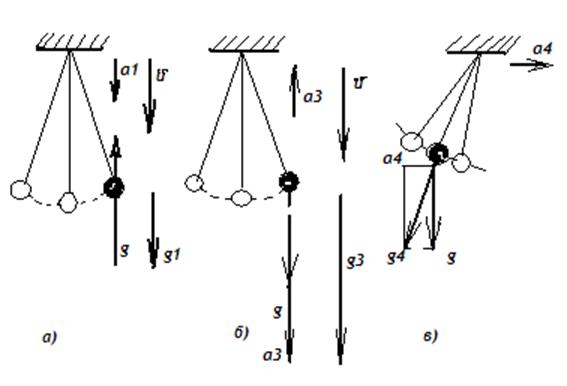
Рисунок 55
Шахмаев 11 кл.
Примеры решения задач
1 Колебательный контур индуктивностью 4000 мкГн и емкостью 400 пФ был подключен к источнику напряжением 400 В. Определите частоту и период свободных колебаний в контуре и амплитудное значение силы тока в контуре. Анализ условия. Задача чисто расчетная: все необходимые величины можно вычислить по известным формулам. Однако надо быть внимательным при подстановке величин в эти формулы: пикофарады и микрогенри надо выразить в фарадах и генри.
Решение.
__ __________________
ω0 = l / √LC = l / √400 · 10-6 · 400 · 10-12 = 2,5 · 106 рад/с;
ν = ω0 / 2π = 2,5 · 106 / 6,28 ≈ 400 · 103 Гц = 400 кГц,
__ _________________
Т = 2π√LC = 6,28√400 · 10-6 · 400 · 10-12 ≈ 2,5 · 10-6 с = 2,5 мкс,
____
Im = √2E/L. Но E = CUm/2
_____ ___________________________
Поэтому Im = Um √C / L = 400 В √ 400 · 10-12 / 400 · 10-6 = 10-3 А
2 Максимальный заряд конденсатора колебательного контура Qm = 1 Кл, а циклическая частота ω0 = 1 рад/с. Чему равна амплитуда колебаний силы тока в контуре?
Анализ условия. Задача сводится к нахождению соотношения между амплитудой тока, амплитудой заряда и циклической частотой.
Решение:
___ ___
Im = Qm / √LC, или Im = Qm · 1 / √LC,
___
Но 1 / √LC = ω. Поэтому Im = Qm ω0
Обратите внимание на полученный результат, он вам в дальнейшем будет нужен.
Вычисление. Im = 1 Кл · 1 1/с = 1 А
Мякишев 11 кл.
Примеры решения задач
1 Максимальный заряд на обкладках конденсатора колебательного контура qm = 10-6 Кл. Амплитудное значение силы тока в контуре Im = 10-3 А. Определите период колебаний. Потерями при нагревании проводников можно пренебречь.
Решение. Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значению энергии магнитного поля катушки:
qm2 / 2C = LIm2 / 2
Отсюда LC = qm2 / Im2,
___
или √LC = qm / Im
___
Следовательно, Т = 2π√LC = 2π · qm / Im ≈ 6,3 · 10-3 с
2 Рамка площадью S = 3000 см2 имеет N = 200 витков и вращается в однородном магнитном поле с индукцией B = 1,5 · 10-2 Тл. Максимальная ЭДС в рамке Em = 1,5 В. Определите время одного оборота.
Решение: Амплитуда ЭДС индукции в одном витке равна BSω. Так как ЭДС, возникающие в отдельных витках рамки, складываются, то для амплитуды ЭДС в рамке, имеющей N витков, получим Em = BSω.Отсюда
ω = Em / NBS
Время одного такого оборота можно найти так:
Т = 2π / ω = 2πNBS / Em ≈ 3,8 · 10-2 с
3 Катушка с индуктивным сопротивлением ХL = 500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100В. Определите амплитуду силы тока Im в цепи и индуктивность катушки L. Активным сопротивлением катушки можно пренебречь.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.