Электротехника \ Теоретические основы электротехники

Расчет трехфазной цепи. Расчет симметричного режима трехфазной цепи, страница 8

 uc=>Uc(p) =F1C(p)/pF2C(p)=> [45,45455*10-9*0 +(4,545455*10-3+18,181818*10-4) *0 +100] /[5*10-9 *02+2*10-4*0+1]+[45,45455*10-9*(-5857,86)2 +(4,545455*10 -3               +18,181818*10-4) *(-5857,86)+100] * e-5857,86t/[(10-8*(-5857,86) +2*10-4 ) *          *(-5857,86)] +[45,45455*10-9 +(4,545455*10-3+18,181818*10-4)*(-34142,1)+100] *e-34142,1t  / [(10-8*(-34142,1)+2*10-4 ) *(-34142,1)]=100-77,5958* e-5857,86t-

-13,3133*e-34142,1t                                                                                                                                                  (2.14a)                                                                                             

Полученные уравнения переходного тока в индуктивности  (2.13a)                                                                                              и переходного напря­жения на конденсаторе  (2.14a)                                                                                              такие же как (2.23) и (2.34). Следовательно, им будут соответ­ствовать диаграммы мгновенных значений, приведенные на рис.2.2 и рис. 2.3.

Часть 3.

РАСЧЕТ ЭЛЕКТРОМАГНИТА

1.1 Исходные данные

1.1.1. Рисунок магнитной цепи (МЦ)  

 Рисунок 1. Рисунок магнитной цепи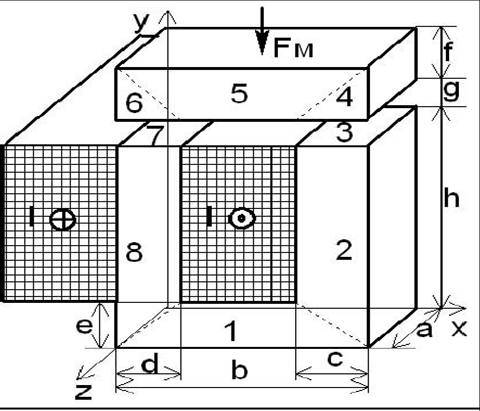

1.1.2. Геометрические размеры (табл. 1).

Таблица 1 – Геометрические размеры

a

b

c

d

e

f

g

h

20

50

20

25

30

25

5

70

1.1.3. Материал участков МЦ и кривые намагничивания (рис. 1.1)

Основания - сталь низкоуглеродистая электротехническая марки Э отожженная;

Якоря - сталь качественная конструкционная марки 10 отожженная;

 Рисунок 1.1 - Кривые намагничивания материалов:

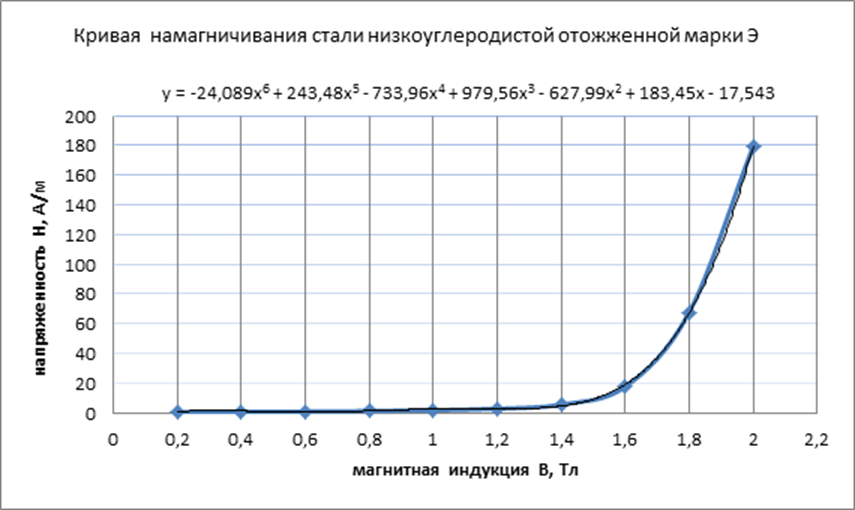
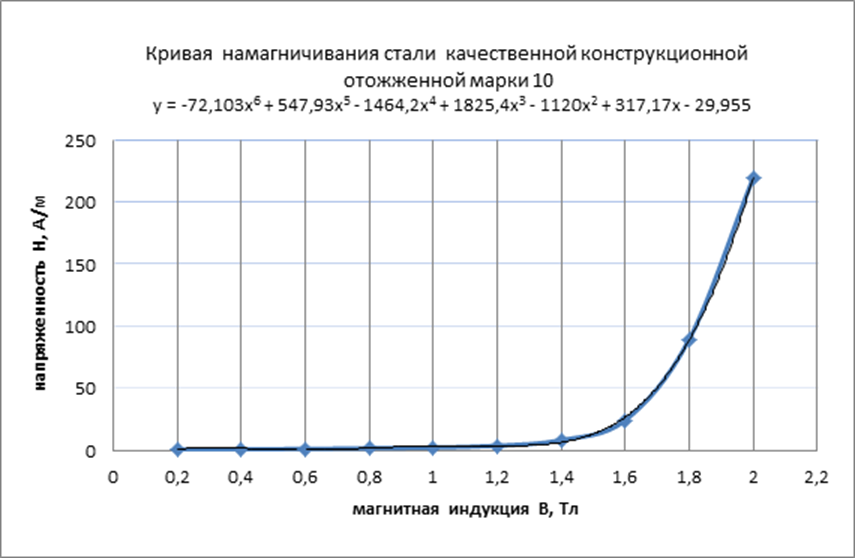
1.1.4 Магнитная индукция на одном из участков МЦ

 B3=1,8Тл

1.1.5 Потребляемый ток I=10 А

1.1.6 Допустимая плотность тока j=4 А/мм2

1.1.7 Удельное сопротивление материала обмотки 0,017 Ом⋅мм2/м

1.2 Прямая задача

Требуется найти

1.2.1 Магнитодвижущую (намагничивающую) силу (МДС)  Iw.

1.2.2 Число витков обмотки w.

1.2.3 Абсолютную магнитную проницаемость участков МЦ μai.

1.2.4 Магнитные сопротивления участков МЦ Rмi и МЦ в целом Rм.

1.2.5 Индуктивность обмотки L

1.2.6 Энергию магнитного поля WM.

1.2.7 Электромагнитную силу FM.

1.2.8 Длину и диаметр провода обмотки lпр и dпр.

1.2.9 Сопротивление обмотки R.

1.2.10 Напряжение питания U.

1.3 Обратная задача

1.3.1 Построить тяговую характеристику по трем точкам (g, g/2, g/4), считая неизменной намагничивающую силу, полученную в прямой задаче.

1.4 Допущения

1.4.1 Материалы магнитной цепи изотропные.

1.4.2 Пренебречь полями рассеяния и выпучивания.

1.4.3 Зазор между обмоткой и якорем электромагнита отсутствует.

1.5 Методические указания

1.5.1 На схемах МЦ (таблица 2) участки пронумерованы. Воздушные          зазоры – это участки под номерами 3 и 7.      зазоры – это участки под номерами 3 и 7.     

1.5.2. Принять, что электромагнитные силы FMi прилагаются в i-тых воздушных зазорах вдоль соответствующих средних линий.

1.5.3. Равнодействующая сила FM приложена к середине якоря;

 1.5.4. В системе двумерного моделирования электромагнитных полей ELCUT магнитную цепь представить сечением, в плоскости симметрии, параллельной плоскости ХУ.

2 Прямая задача (расчет электромагнита)

В основе расчета магнитной цепи лежит закон полного тока, который для МЦ, разбитой на участки с однородными магнитными свойствами, примет вид

F=Iw=§Hdl=ili=iRMi=iSiRMi=

Поскольку магнитные сопротивления ферромагнитных участков нелинейные, то используется графоаналитический метод расчета при решении и прямой и обратной задачи. Графически по кривым намагничивания определяются напряженности магнитного поля, все остальные расчеты – аналитические.

2.1 Исходные данные

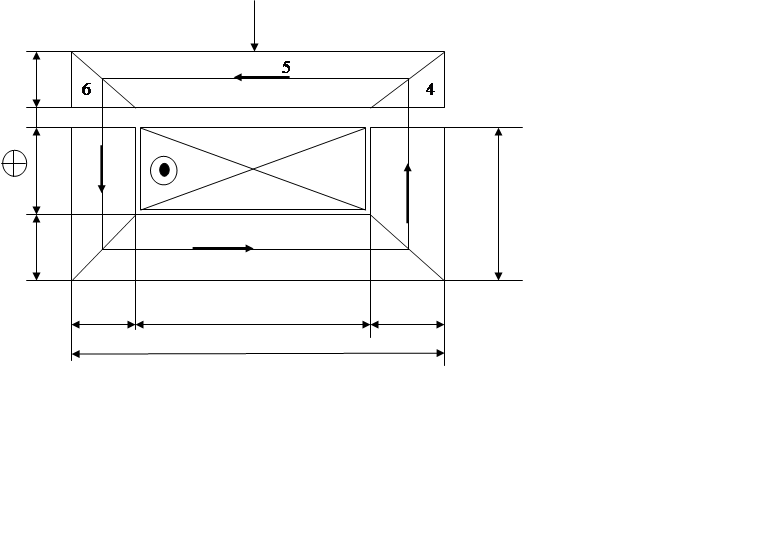
2.1.1 Расчетная схема МЦ строится в плоскости симметрии, в которой распространяется магнитный поток Ф. (рисунок 2.1).

 


Скачать файл