Расчет трехфазной цепи. Расчет симметричного режима трехфазной цепи, страница 6

Решение u_С, ЛН ОДУ (2.24), состоящее из частного u_CПР (2.11) и общего u_ССВ (2.33) решений, имеем в виде                                                                       

u_С= u_CПР +u_ССВ=100-77,5967515  e^{-5857,86 t} - 13,3131585 e^-34142,1t В       (2.34)

2.6. Диаграммы напряжения и тока (рис.2.2 и2.3) строятся согласно (2.23)и (2.34)по завершении переходного процесса , в диапазоне t=0...4τ, где постоянная времени τ=1/α=1/5857=0.00017с    t=0,00068с.                (2.35)   

t,c                i,A                   t,c                i,A                t,c                i,A                                                                                                                            

0	4,5455
0,000025	2,9309
0,00005	2,1077
0,000075	1,6399
0,0001	1,3395
0,000125	1,1242
0,00015	0,9571
0,000175	0,8207
0,0002	0,7063
0,000225	0,6090
0,00025	0,5255
0,000275	0,4537
0,0003	0,3918
0,000325	0,3383
0,00035	0,2922
0,000375	0,2524
0,0004	0,2180
0,000425	0,1883
0,00045	0,1626
0,000475	0,1404
0,0005	0,1213
0,000525	0,1048
0,00055	0,0905
0,000575	0,07815
0,0006	0,06750
0,000625	0,05830
0,00065	0,05036
0,000675	0,04349

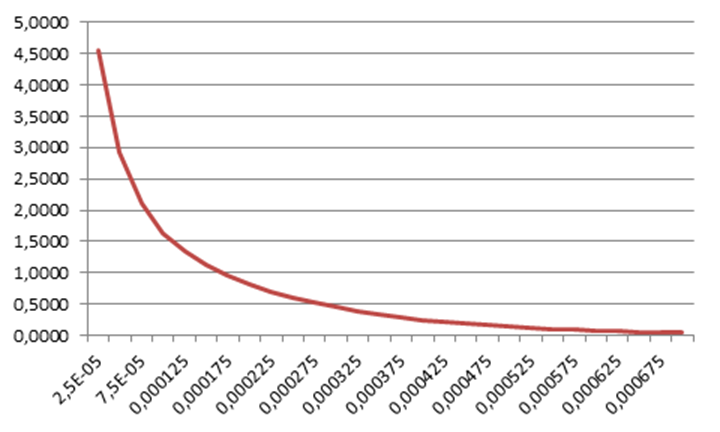
рис.2.2 Диаграмма токов

            t,c                u_С, В                        t,c                u_С, В              

0	9,0901	0,000375	91,3736
0,000025	27,3041	0,0004	92,5487
0,00005	39,6901	0,000425	93,5638
0,000075	48,9634	0,00045	94,4406
0,0001	56,3663	0,000475	95,1980
0,000125	62,5023	0,0005	95,8521
0,00015	67,6922	0,000525	96,4172
0,000175	72,1282	0,00055	96,9053
0,0002	75,9400	0,000575	97,3269
0,000225	79,2239	0,0006	97,6910
0,00025	82,0569	0,000625	98,0056
0,000275	84,5024	0,00065	98,2773
0,0003	86,6141	0,000675	98,5119
0,000325	88,4378	0,0007	98,7147
0,00035	90,0130	0,000725	98,8898

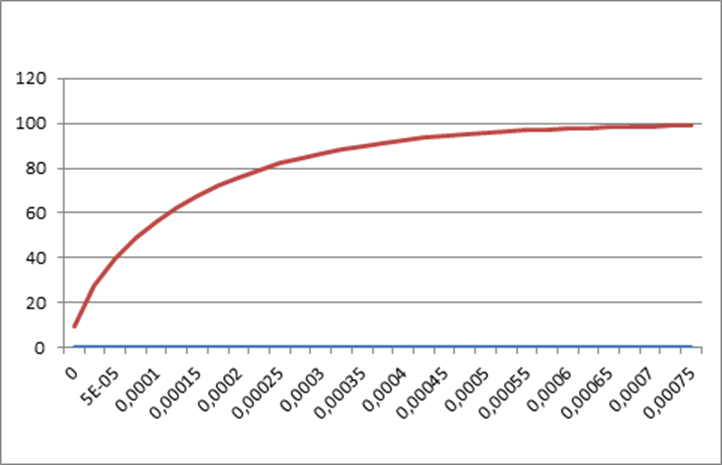
Рис 2.3. Диаграмма напряжений

2.1а. Анализ переходных процессов в RLC-цепи постоянного тока операторным методом

2.1а .1. Независимые начальные условия (ННУ)-токи в индуктивностях и напряжения на конденсаторах до коммутации- определяются также как и в классическом методе. По за­кону Ома (рис. 2.1а) Поскольку сопротивление катушки индуктивности постоянному току равно нулю и при замкнутом ключе S ток протекает от источника ЭДС Е через резисторы R1 и R4, то по закону Ома ток в индуктивности

i_L(0-)=E/(R1+R4)=100/(20+2)= 4,545455 А                                   (2.1а)

а напряжение на конденсаторе

u_C(0-)=U_R4=R*iR(0-)=2*4,545455 = 9,090909 в.                            (2.2а)

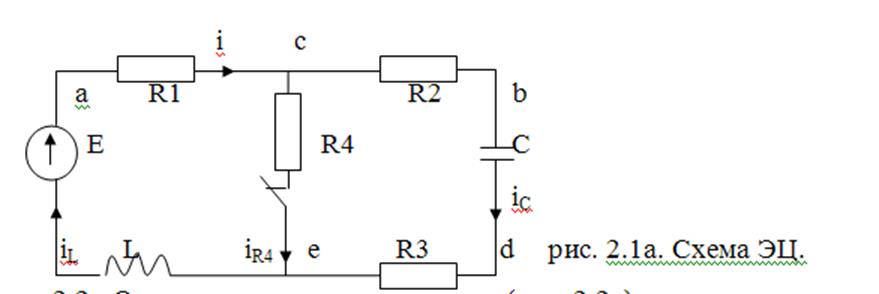
2.2а Операторная схема замещения(рис. 2.2а) состав­ляется для цепи после коммутации. Операторные сопро­тивления индуктивности и конденсатора равны Lp и 1/Ср.Начальные условия - ток в индуктивности i_L(0-) и напря­жение на конденсаторе u_C(0-) до коммутации - учитывают­ся в виде источников Li_l(0)и u_C(0)/p.При этом направле­ние источника, учитывающего ток в индуктивности, совпадает с направлением тока, а направление источника, отражающего напряжение на конденса­торе, - противоположно току в конденсаторе- Источник ЭДС Е имеет изображение Е/Р.