Расчет трехфазной цепи. Расчет симметричного режима трехфазной цепи, страница 4

	Таблица		2.1	Параметры			элементов		цепи
№                      L							R1          R2             R3			R4
№	рис.	В	мГн		С, мкФ		Ом
I	5	100	3	1	Р	10	20	15	5	2

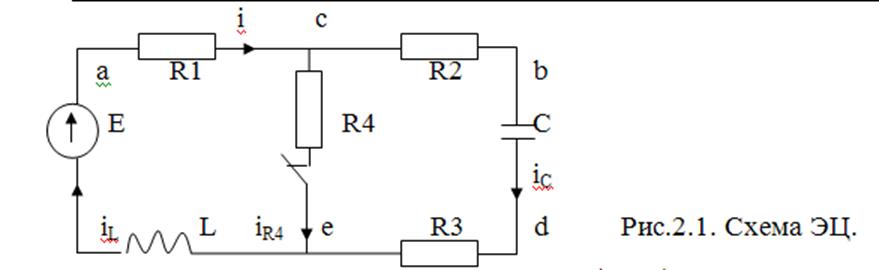
2.1 Независимые начальные условия (ННУ) — токи в индуктивностях и напряжения на конденсаторах - определяются для электрической цепи (ЭЦ) до коммутации. Поскольку сопротивление катушки индуктивности постоянному току равно нулю и при замкнутом ключе S ток протекает от источника ЭДС Е через резисторы R1 и R4, то по закону Ома ток в индуктивности

i_L(0-)=E/(R1+R4)=100/(20+2)= 4,545455 А                                   (2.1)

а напряжение на конденсаторе

u_C(0-)=U_R4=R*iR(0-)=2*4,545455 = 9,090909 в.                            (2.2)

2.2 Дифференциальные уравнения. Для цепи после коммутации по второму закону Кирхгофа:

         u_С+u_L+u_R1+R2+R3=E;                                                                      (2.3)                                                                       

Компонентные уравнения

           u_L=Ldi_L/dt;                                                                                 (2.4)                                                                                                                                                                                                                                          

          i_C=Cdu_C/dt.                                                                                          (2.6)                                                                                                                                                                                         u_R1+R2+R3 =(R1+R2+R3)*i_R                                                                                                (2.7)

         i_R = u_R1+R2+R3/(R1+R2+R3)                                                                                                   (2.8)

 Решение i_{L_} ЛН ОДУ состоит из частного решения (ЧР) ЛН ОДУ - i_LПР и общего реше­ния (OP)  i_LСВ линейного однородного (ЛО) ОДУ, т.е.

i_L =  i_LПР+ i_LСВ                                                                                                   (2.9)

Частное решение или принужденная составляющая обусловлена действием источников энергии и не зависит от времени, а общее решение — свободная составляющая обусловлена перераспределением энергии в накопителях - в катушках индуктивностей и конденсаторах и не зависит от источников энергии.

2.3 Частное решение i_LПР ЛН ОДУ определяется, когда переходные процессы завер­шатся (т.е. при t—∞) и в цепи будет протекать постоянный ток

       i_LПР (0+) =0 A;                                                                                  (2.10)

       u_СПР(0+) =Е=100В.                                                                           (2.11)                                                                          

2.4 Общее решение i_LСВ для ЛО ОДУ зависит от корней характеристического уравнения (ХУ).

2.4.1 Характеристическое уравнение  p² LC+p(R1+R2+R3)C+1 =0    или

p² *10^-3+p(20+15+5)+1=0                                                                      (2.12)

имеет корни 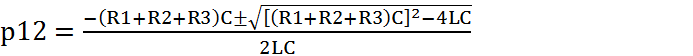(2.13)

p₁= -5857,86 с^-1                                                                                                 (2.14)

p₂= -34142,1с^-1                                                                                                 (2.15)

Поскольку корни ХУ действительные сопряженные, то переходный процесс будет зату­хающим и общее решение ищется в виде

i_LСВ (0+)=A₁e^p1t+ A₂e^p2t                                                                                                                                        (2.16)

2.4.2 Зависимые начальные условия.