Расчет трехфазной цепи. Расчет симметричного режима трехфазной цепи, страница 3

UЭa=UA-ΔUЛА-UnэN=110-(16,8766+36,0062j)-(54,9470-10,9830j)=38,1764-

-25,0231j B;

UЭb=UB-ΔUЛB-UnэN=110e^-j120-(-74,9277+14,9768jB)-(54,9470-10,9830j)=-35,0193-

-99,2566j B;

UЭc=UC-ΔUЛC-U_nэN=110e^j120-(-106,7899-18,0339j)-(54,9470-10,9830j)=-3,1571++124,2798j B

22 Линейные напряжения нагрузки

Uab=UЭa-UЭb=(38,1764-25,0231j)-( -35,0193-99,2566j)=73,1956+74,2335j B;

Ubc=UЭb-UЭc=(-35,0193-99,2566j)-( -3,1571+124,2798j)=-31,8622-223,5364j B;

Uca=UЭc-UЭ a=(-3,1571+124,2798j)-( 38,1764-25,0231j)=-41,3335+149,3029j B.

23 Фазные и линейные токи треугольника и звезды нагрузки

Iab=Uаb/Zab=(73,1956+74,2335j)/( 90-90j)= -0,0058+0,8191j A;

Ibc=Ubc/Zbc=(-31,8622-223,5364j)/( 90-90j)= 1,0649-1,4189j A;

Ica=Uca/Zca=(-41,3335+149,3029j)/( 90-90j)=-1,0591+0,5998j А;

I aт=Iab-Ica=(-0,0058+0,8191j)-( -1,0591+0,5998j)= 1,0533+0,2192j A;

Ibт=Ibc-Iab=(1,0649-1,4189j)-( -0,0058+0,8191j)= 1,0706-2,2379j A;

Icт=Ica-Ibc=(-1,0591+0,5998j)-( 1,0649-1,4189j)= -2,1239+2,0187j A.

Ia=IА-Iaт=(1,3639-0,6393j)-( 1,0533+0,2192j)=0,3105-0,8585j A;

Ib=IB-Ibт=(-0,6808-3,4058j)-( 1,0706-2,2379j)=-1,7514-1,1679j A;

Ic=IC-Icт=(-0,6831+4,0451j)-( -2,1239+2,0187j)=1,4408+2,0264j A.

 

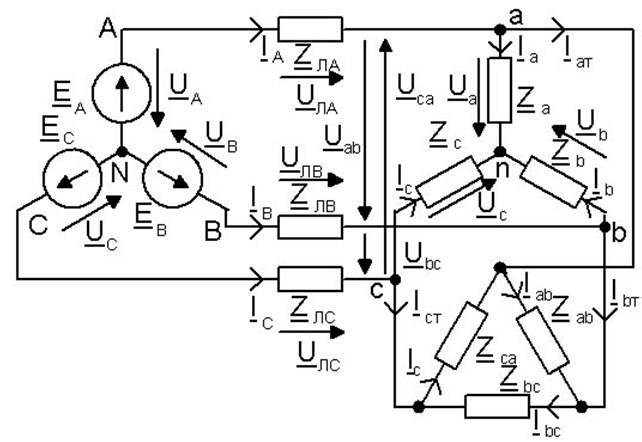
Рисунок 9 – К расчету напряжений и токов

24 Проверка решения по балансу мощностей.

24.1 Мощность источников

ŠИ=ŠEA+ŠEВ+ŠEС=UAǏA+UBǏB+UCǏC=110(1,3639+0,6393j)+110e^-j120(-0,6808+3,4058j)+

+110e^j120(-0,6831-4,0451j)=-484,7530-105,7017j=496,14e^-j167,70  BA.

24.2 Мощность потерь в линии и мощность нагрузки

ŠH=ŠZЛ+ŠZЗ+ŠZТ=I²AZЛА+I²ВZЛВ+I²СZЛС+ I²aZa+I²bZb+I²cZc+ I²abZab+I²_caZ_ca+I²bcZbc=

=1,5063²(26,4j)+3,4732²(-22j)+4,1023²(26,4j)+0,91²(40+30j)+2,11²(40+30j)+

+2,49²(40+30j)+0,82² (90-90j)+ 1,77² ( 90-90j)+ 1,22² ( 90-90j)=-484,7530-   

-105,7017j=496,14e^-j167,70 BA.

24.3 Погрешности расчета полной γS, активной γP, реактивной γQ мощностей и

 фазы γφ.

γS =(SИ – SH)/SИ =(-496,14+496,14)/(-496,14)=0

γP =(PИ – PH)/PИ =(-484,7530+484,7530)/( -484,7530) =0;

γQ =(QИ –QH)/QИ=(-105,7017+105,7017)/( -105,7017)=0 ;

γφ =(φИ –φH)/ φИ=(-167,70 +167,70)/ (-167,70) =0.

25 Векторная диаграмма токов и топографическая диаграмма напряжений (рисунок10) строится в следующем порядке.

25.1 На комплексной плоскости, повернутой на 900 против часовой стрелки, строятся векторы фазных UA, UB, UC и линейных UAB, UBC, UCA напряжений генератора. Затем векторы фазных Ua, Ub, Uc и линейных Uab, Ubc, Uca напряжений нагрузки и падений напряжений на сопротивлениях линии ΔUЛB, ΔUЛC, ΔUЛA. При этом должен выполняться второй закон Кирхгофа для соответствующих контуров напряжений (рисунок 10)

UAB=UA–UB, UBC=UB–UC, UCA=UC–UA,

Uab=Ua-Ub, Ubc=Ub-Uc, Uca=Uc-Ua,

UA=Ua+ΔUЛA, UB=Ub+ΔUЛB, UC=Uc+ΔUЛC.

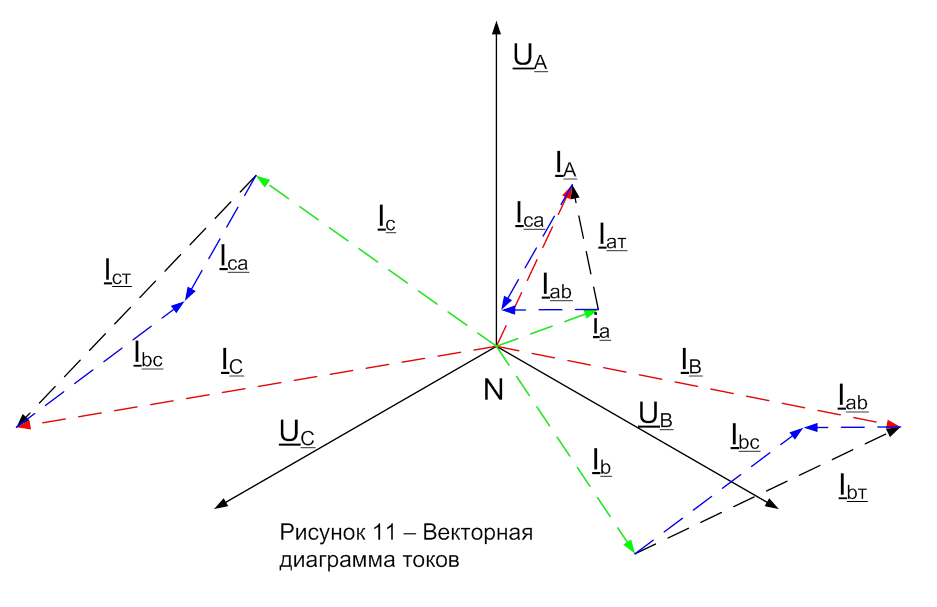
12.2 При построении векторов линейных токов генератора IA, IB, IC нужно учитывать,что при индуктивной нагрузке генератора ZA токи отстают по фазе от фазных напряжений генератора UA, UB,UC, а по первому закону Кирхгофа IA+IB+IC=0.

Векторы фазных токов Ia,Ib, Ic при активно-индуктивном сопротивлении фаз звезды нагрузки Zа отстают от фазных напряжений Ua, Ub, Uc и сумма токов Ia+Ib+Ic=0.

По первому закону Кирхгофа для узлов а, b и c линейный ток генератора равен сумме фазного тока звезды и линейного тока треугольника нагрузки IA=Ia+Iaт, IВ=Ib+Ibт, IC=Ic+Icт ,линейные токи треугольника разности его фазных токов Iат=Iab-Ic

а линейные токи треугольника разности его фазных токов Iат=Iab-Ic,Ibт=Ibс-Iаb,Iст=Icа+Iвс  (рисунок 11).

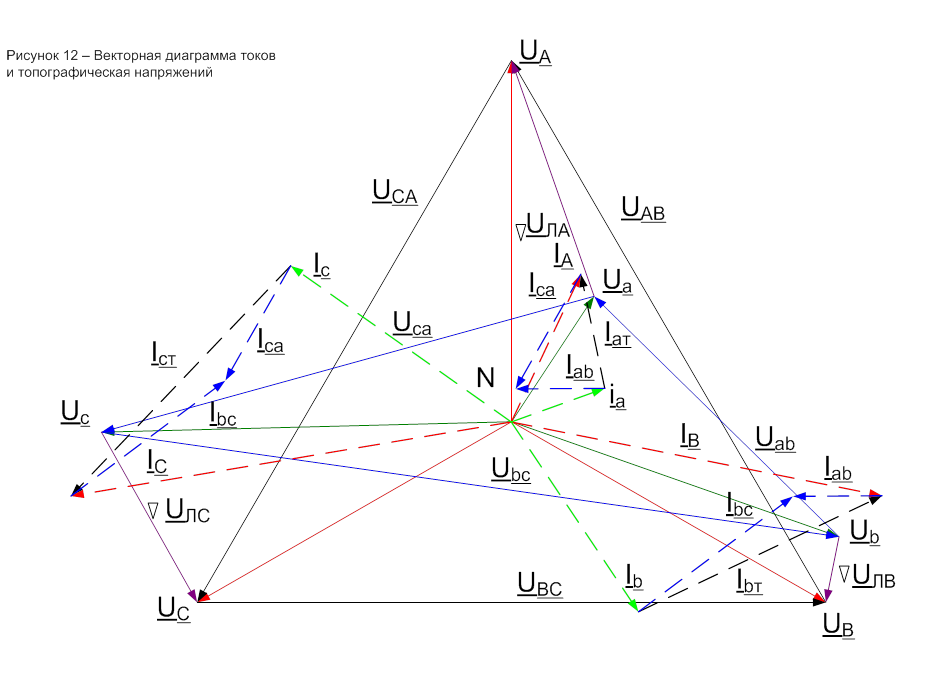
При индуктивной нагрузке фазные токи треугольника отстают от фазных напряжений на 90⁰ (рисунок 12).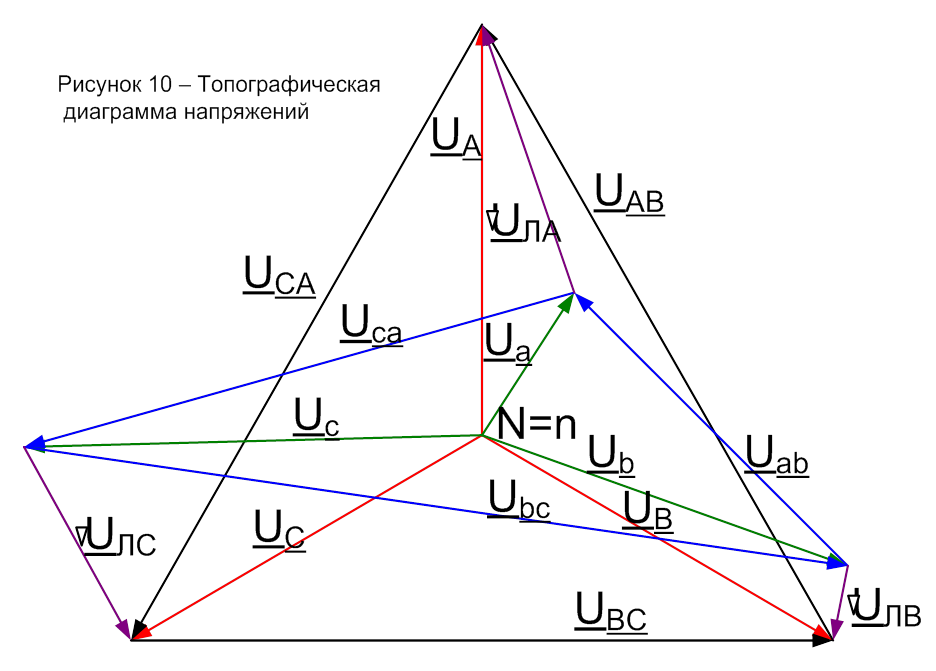

Часть 2.

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Задание: С источником ЭДС постоянного тока найти классическим методом токи и напряжения на индуктивности и конденсаторе в RLC-цепи.

Построить диаграммы для t=0…4 τ =0...4/|Pmin|

Операторный метод применить для: RLC-цепи постоянного тока.

Схемы ЭЦ и значения параметров приведены в таблице 1 и рис.1.