2.13.2 Для повышения к.п.д. следует уменьшить магнитное сопротивление воздушного зазора на участке № 3 за счет увеличения площади и уменьшения длины зазора. При линейной зависимости магнитного сопротивления воздушного зазора от геометрических размеров, увеличение площади и/или уменьшение длины воздушного зазора в 2 раза приведет к уменьшению энергии в 4 / или в 2 раза.
3 Обратная задача (построение тяговой характеристики электромагнита)
После подачи напряжения питания на обмотку электромагнита якорь начинает движение. Это приводит к уменьшению воздушного зазора, и, следовательно, к уменьшению его магнитного сопротивления.
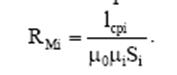
При неизменной магнитодвижущей силе Iw возрастет магнитный поток.
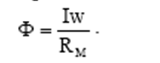
В результате возрастания магнитного потока возрастет магнитная индукция в зазорах и. естественно, электромагнитная сила Fm- Решив обратную задачу для нескольких значений воздушного зазора g можно построить тяговую характеристику электромагнита Fм=f(g).
3.1 Стратегия (алгоритм) решения
3.1.1 Для уменьшенной величины воздушного зазора (например g/2) задаются произвольным значением магнитной индукции Вil на каком либо i-том участке. Поскольку магнитное сопротивление уменьшится, следовательно, нужно задать большее значение магнитной индукции на этом участке, по сравнению с прямой задачей. При этом задаваемая индукция не может превышать индукцию насыщения материала участка Вi.
3.1.2 Решается прямая задача и для заданной индукции определяется намагничивающая сила Iwi.
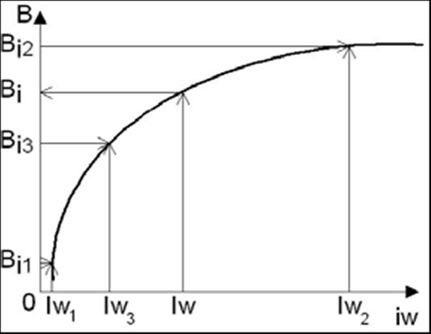
Рисунок 3.1
3.1.3 Строится диаграмма зависимости магнитной индукции МДС В=f(Iw) (рисунок 3.1), на которую наносятся значения магнитной индукции и МДС, полученные при решении прямой задачи при уточненном расчете (Вi и Iw из таблицы 4) и на первом шаге (первом приближении) обратной задачи (Вi1 и Iw1).
3.1.4 Сравнивается найденное значение Iw1 с МДС обмотки Iw. В зависимости от их взаимного положения принимается решение о значении магнитной индукции Вi2 на следующем шаге (втором приближении) с учетом условий по пп 3.1.1.
3.1.5 На следующем шаге решения обратной задачи повторяются пп 3.1.2 – 3.1.4 до тех пор, пока МДС электромагнита Iw не будет на внутреннем участке зависимости В=f(Iw), что даст возможность интерполяции. Ввиду нелинейной зависимости В=f(Iw) экстраполяция(определение значения функции вне графика) приводит к большей погрешности по сравнению с интерполяцией.
3.1.6 После определения в результате интерполяции искомого значения магнитной индукции выполняется уточняющий расчет для определения индукции в воздушных зазорах и расчета тягового усилия электромагнита Fм(g/ 2).
3.1.7 Для следующего значения длины воздушного зазора (g/4) повторяются пп. 3.1.1 — 3.1.6 и определяется электромагнитная сила Fм|(g/4)s Rм(g/4) и индуктивность L(g/4).
3.1.8 Строится тяговая характеристика электромагнита FM=f(g) (рисунок 3.2).
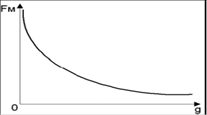Рисунок 3.2 - Тяговая характеристика электромагнита F
3.2 Шаг1
Длина участка № 7 уменьшается в два раза (l7=g/2).
Значение индукции целесообразно задавать на участках с большим сечением и меньшей индукцией. Например, на участке № 1 можно принять индукцию B1=1.3 Тл. Для новых значений l7 и В1решается прямая задача.
3.2.1 Пересчитывается магнитная индукция (пп.2.2), которая не должна превышать индукцию насыщения.
3.2.2 Дли новых значений индукции по кривым намагничивания определяются напряженности магнитного поля (пп.2.3).
3.2.3 Вычисляются магнитные напряжения (пп.2.4).
3.2.4 Определяется МДС (пп.2.5).
Таблица 5 – Результаты расчетов на первом шаге (при g/2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.