МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА ЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРООБОРУДОВАНИЯ ПРЕДПРИЯТИЙ
Курсовая работа
по Теоретическим основам электротехники
Выполнил: студент гр.АЭз-05-01
Абизгильдин Р. А.
Шифр: 073743
Проверил: доцент Чигвинцев С.В.
Уфа 2008
Часть1.
РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ
1 Исходные данные
1.1 Исходная схема
трехфазной электрической цепи (рисунок 1).
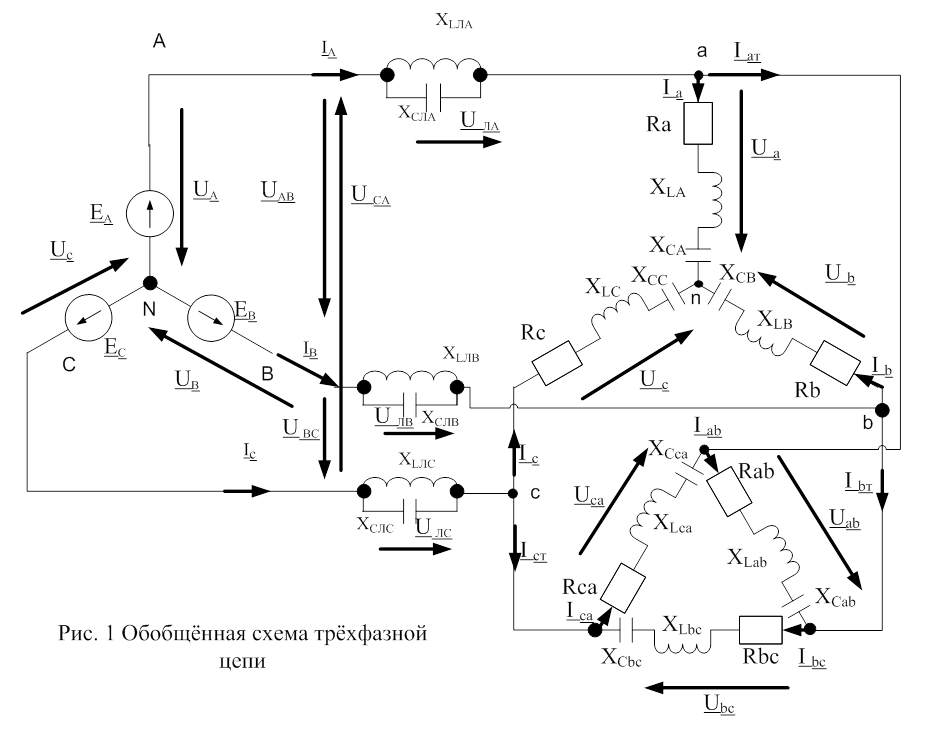
1.2 Действующее значение ЭДС фазы А E=110 B.
1.3 Сопротивления фаз:
- линейных проводов RЛ=RЛА=![]() Ом;ХLЛА=ХLЛ=12
Ом; ХСЛА=ХСЛ=22 Ом;
Ом;ХLЛА=ХLЛ=12
Ом; ХСЛА=ХСЛ=22 Ом;
- звезды нагрузки Ra=RЗ=40 Ом; XLa=XLЗ=70 Ом; ХСа=ХСЗ=40 Ом;
- треугольника нагрузки Rab=RТ=90 Ом; XLТ=120 Ом; ХСТ=210 Ом.
В несимметричном режиме Rb= ![]() .
.
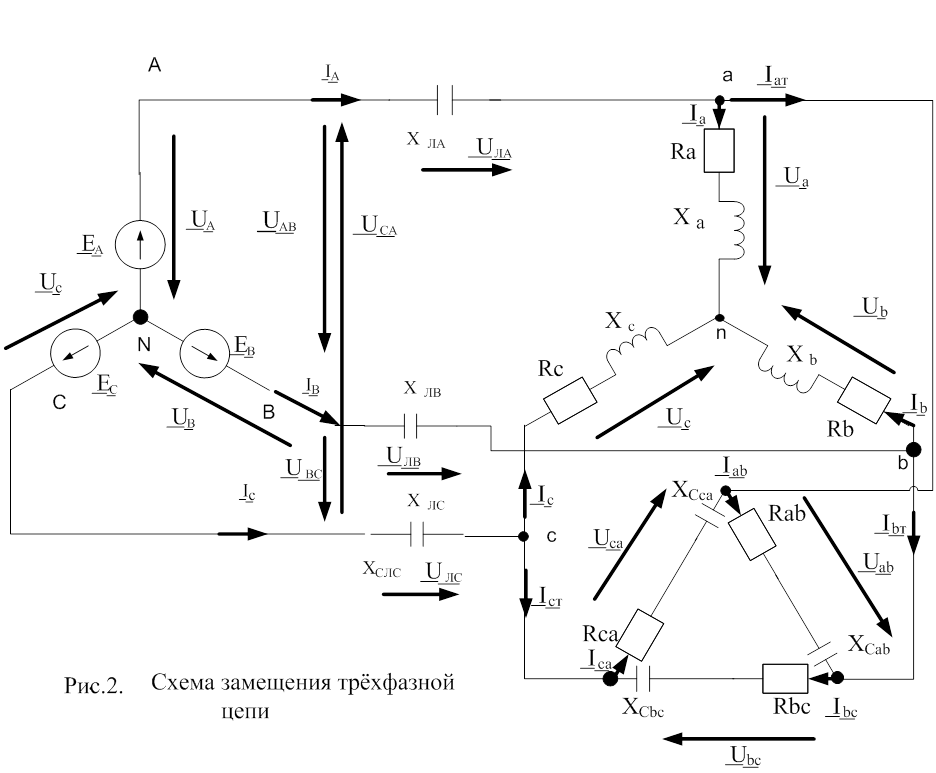
РАСЧЕТ СИММЕТРИЧНОГО РЕЖИМА ТРЕХФАЗНОЙ ЦЕПИ
2.1 Сопротивления фаз линии при параллельной схеме замещения
ХЛ=[jXLЛ*(-jXCЛ)]/(jXLЛ-jXCЛ)=[j12*(-j22)]/(j12-j22)=j 26,4Ом.
2.2 Комплексное сопротивление фазы линии для последовательной схемы замещения
ZЛ=ZЛА=1/(1/RЛ+1/jXLЛ-1/jXCЛ)=1/(1/![]() +1/j12-1/j22)= 26,4jОм.
+1/j12-1/j22)= 26,4jОм.
2.3 Комплексное сопротивление фазы звезды нагрузки
ZЗ=Zа=RЗ+jXLЗ-jXCЗ=40+j70-j40=Rа+jXа=40+30j Ом.
2.4 Комплексное сопротивление фазы треугольника нагрузки
ZT=Zab=RT+jXLT-jXCT=Xab=90+j120-j210=90-j90 Ом.
Как следует из расчета сопротивление линии индуктивное, а фаз звезды и треугольника нагрузки соответственно активно-индуктивное и активно-емкостное.
4 При симметричной нагрузке достаточно рассчитать одну из фаз, например, фазу А, а затем использую фазные множители а2=e-j120 и а=ej120
найти напряжения и токи в других фазах В и С.
4.1 Треугольник нагрузки необходимо преобразовать в эквивалентную звезду ZЗЭТ=Zтa=ZTZT/(ZT+ZT+ZT)=(90-j90 )/3=30-j30 Ом.
4.3 Сопротивление фазы А
|
ZA=ZЛА+1/(1/Zа+1/Zта)=(-j26,4)+1/[(40+30j)+1/( 30-j30)]= 30+22,1142j Ом |
4.2 Схема замещения одной фазы (фазы А) трехфазной цепи (рисунок 3).
5 Линейный (фазный) ток фазы А
IA=UA/ZА=110/(30+22,1142j)= 2,3757-1,7513j A.
Токи в фазах В и С через фазные множители
IB =a2IA= e-j120(2,3757-1,7513j)= -2,7045-1,1818j A;
IC =aIA =ej120(2,3757-1,7513j)= 0,3288+2,9331j A.
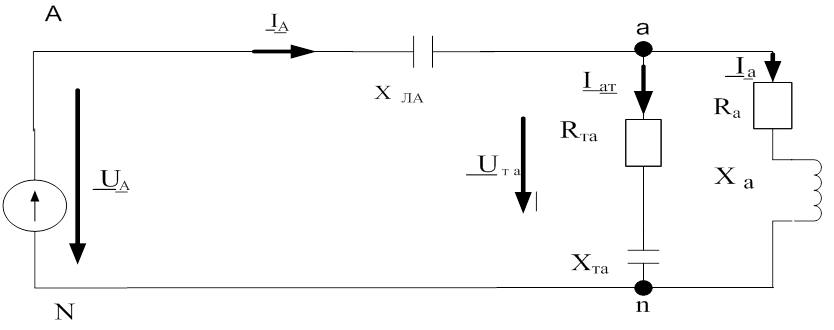
рис. 3. Схема замещения фазы А.
6 Вычислить падение напряжения на сопротивлении линейного провода фазы А
ΔUЛА= IAZЛ=(2.68-j3.19)(7.90-j0.87)= 46,2332+62,71950j B.
Падение напряжений на сопротивлениях линий фаз В и С
ΔUЛВ= а2IA=e-j120(46,2332+62,71950j)= 31,2001-71,3989j B;
ΔUЛС= аIA= ej120(46,2332+62,71950j)= -77,4333+8,6794j B.
7 Напряжение на фазе a звезды нагрузки
Uа=UА-ΔUЛА=110–(46,2332+62,71950j)= 63,7668-62,7195j B.
Напряжения на фазах b и c
|
Ub =a2Ua= e-j120(63,7668-62,7195j)= 22,4333+86,5834j В. |
|
|
Uc=aUa =ej120(63,7668-62,7195j)= -86,2001-23,8639j В |
|
8 Токи в фазе a звезды нагрузки
Ia=Ua/Zа=(63,7668-62,7195j)/( 40+30j)= 0,2676-1,7687j A.
Фазные токи в фазах a и c звезды нагрузки
Ib =a2Ia= e-j120(0,2676-1,7687j)= 1,3979+1,1161j A;
Ic =aIa =ej120(0,2676-1,7687j)= -1,6656+0,6526j A.
9 Линейный ток фазы a треугольника нагрузки
Iaт=IА-Ia=(2,3757-1,7513j)-( 0,2676-1,7687j)= 2,1081+0,0175j A.
Линейные токи фаз b и c треугольника нагрузки
|
Ibт= a2Iaт= e--j120(2,1081+0,0175j)= -1,0692+1,8169j А; |
Icт= aIaт= ej120(2,1081+0,0175j)= -1,0389-1,8344j A.
10 Фазный ток фазы аb треугольника нагрузки
Iab=Iaт/√3e-j30=(2,1081+0,0175j)/(√3e-j30)= 1,0490+0,6173j A.
Фазные токи фаз bс и са треугольника нагрузки
Ibс =a2Iab= e-j120(1,0490+0,6173j)= -1,0591+0,5998j A;
Ica =aIab =ej120(1,0490+0,6173j)= 0,0101-1,2171j A.
11 Проверка решения по балансу мощностей.
11.1 Мощность источников
ŠИ=3ŠEA=3UAǏA=3*110(2,3757-1,7513j)= 783,9938-577,91541j=
= 973,9777ej -36,3955 BA.
11.2 Мощность потерь в линии и мощность нагрузки
ŠH=3(ŠZЛA+ŠZа+ŠZab)=3(I2AZЛА+I2aZa+I2abZab)=3[2,952(26,4j)+1,79 2(40+30j)+1,222 *(90-j90)]= 783,9938+577,91541j=973,9777ej-36,39552 BA.
11.3 Погрешности расчета полной γS, активной γP, реактивной γQ мощностей и фазы γφ
γS =(SИ – SH)/SИ =(973,9777-973,9777)/ 973,9777=0;
γP =(PИ – PH)/PИ =(783,9938-783,9938)/ 783,9938=0;
γQ =(QИ –QH)/QИ=(577,91541-577,91541)/ 577,91541=0;
γφ =(φИ –φH)/ φИ=(36,39552 -36,39552)/ 36,39552 =0.
12 Векторная диаграмма токов и топографическая диаграмма напряжений (рисунок 4) строится в следующем порядке.
12.1 На комплексной плоскости, повернутой на 900 против часовой стрелки, строятся векторы фазных UA, UB, UC и линейных UAB, UBC, UCA напряжений генератора. Затем векторы фазных Ua, Ub, Uc и линейных Uab, Ubc, Uca напряжений нагрузки и падений напряжений на сопротивлениях линии ΔUЛB, ΔUЛC, ΔUЛA. При этом должен выполняться второй закон Кирхгофа для соответствующих контуров напряжений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.