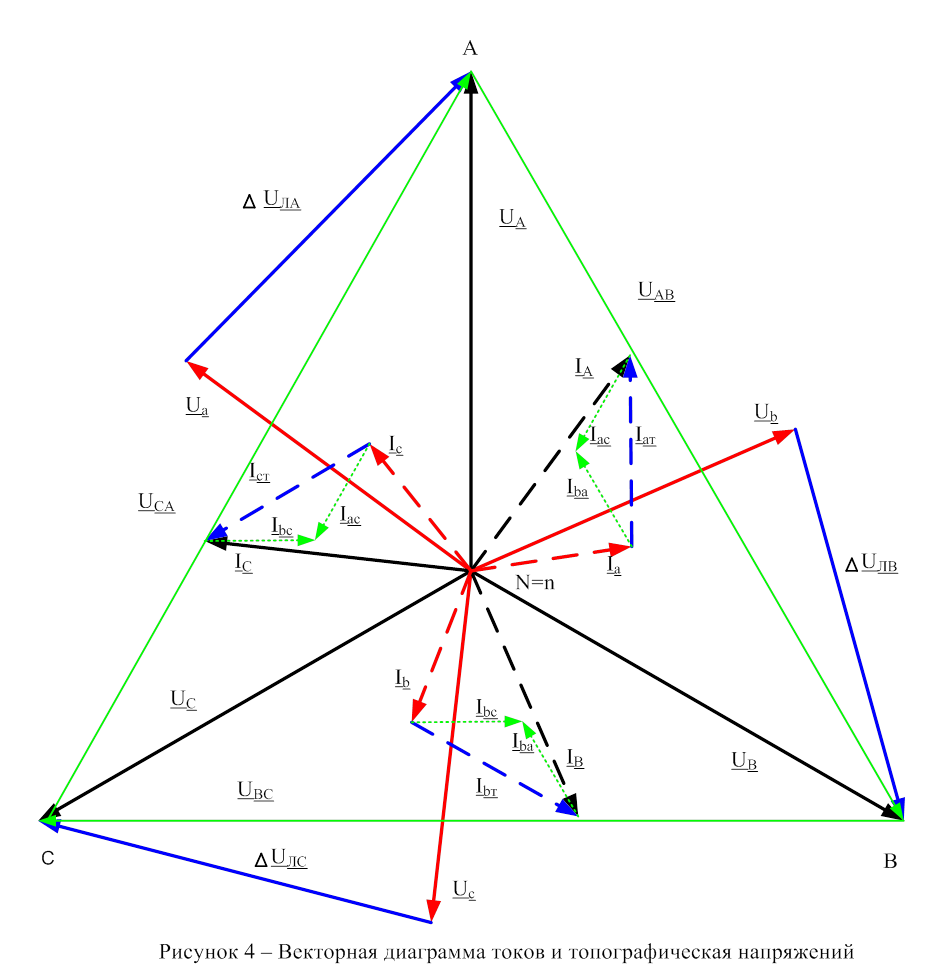
UAB=UA–UB, UBC=UB–UC, UCA=UC–UA,
Uab=Ua-Ub, Ubc=Ub-Uc, Uca=Uc-Ua,
UA=Ua+ΔUЛA, UB=Ub+ΔUЛB, UC=Uc+ΔUЛC.
12.2 При построении векторов линейных токов генератора IA, IB, IC нужно учитывать, что при активно-индуктивной нагрузке генератора ZA и токи отстают по фазе от фазных напряжений генератора UA, UB, UC, а по первому закону Кирхгофа IA+IB+IC=0.
Векторы фазных токов Ia, Ib, Ic при активно-индуктивном сопротивлении фаз звезды нагрузки Zа отстают фазных напряжений Ua, Ub, Uc и сумма токов Ia+Ib+Ic=0.
По первому закону Кирхгофа для узлов а, b и c линейный ток генератора равен сумме фазного тока звезды и линейного тока треугольника нагрузки IA=Ia+Iaт, IВ=Ib+Ibт, IC=Ic+Icт , а линейные токи треугольника разности его фазных токов Iат=Iab-Ica, Ibт=Ibс-Iаb, Iст=Icа+Iвс. При ёмкостной нагрузке фазные токи треугольника опережают фазные напряжения на 900.
РАСЧЕТ НЕСИММЕТРИЧНОЙ ТРЕХФАЗНОЙ ЦЕПИ
13 Несимметричный режим трехфазной цепи обусловлен отсутствием в линии В индуктивности (XLВ=∞), следовательно, комплексные сопро-тивления треугольника и звезды нагрузки останутся прежними (пп. 2.1 – 2.3).
13.1 Комплексные сопротивления фаз линии для последовательной схемы замещения
ZЛА=ZЛС=26,4j Ом и ZЛB= -22j Ом
13.2 Комплексные сопротивления фаз звезды нагрузки
ZЗ=Zа=Zb=Zс= 40+30jОм.
13.3 Комплексные сопротивления фаз треугольника нагрузки
Zab= Zbc =Zca=90-90j Ом
14. Поскольку необходимо определить 12 токов трехфазной цепи, то непосредственное использование законов Кирхгофа и методов контурных токов и узловых потенциалов приведет к системам из 12, 5 и 7 уравнений соответственно. С целью упрощения расчетов, следует воспользоваться методом свертывания электрической цепи рассчитать сопротивления, напряжения и токи в следующей последовательности:
- перейти от звезды нагрузки к эквивалентному треугольнику;
- заменить два параллельно соединенных треугольника одним эквивалентным;
- преобразовать эквивалентный треугольник в эквивалентную звезду;
- найти напряжение между нейтралями генератора и эквивалентной звезды по методу узловых потенциалов;
- определить линейные токи генератора;
- рассчитать падения напряжений в линиях и фазные (линейные) напряжения
эквивалентной нагрузки;
- определить фазные и линейные токи треугольника и звезды нагрузки;
в ходе расчета напряжений и токов проверять выполнение законов Кирхгофа.
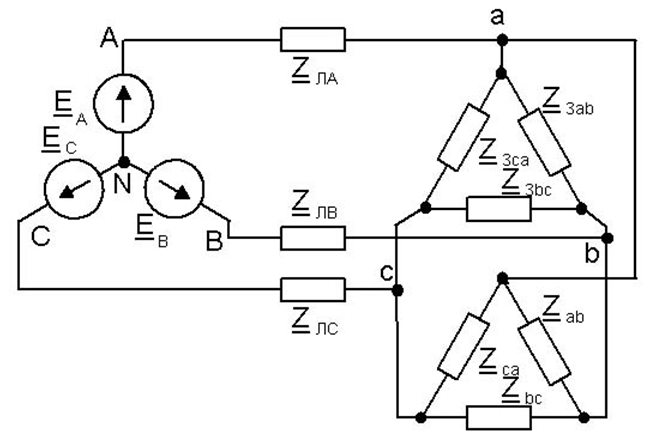
Рисунок 6 – Замена звезды нагрузки треугольником
15 Сопротивления фаз треугольника эквивалентного звезде нагрузки будут равными
ZЗT=ZЗab=ZЗbc=ZЗса=Zа+Zb+ZаZb/Zс=3Zа=3(40+30j)=120+90j Ом.
16 Сопротивления фаз параллельно соединенных треугольников
ZЭab=ZЭbc=ZЭca =ZЗаbZab/(ZЗаb+Zab)=(120+90j)( 90-90j)/[( 120+90j)+ (90-90j)]=
= 90-12,8571j Ом;
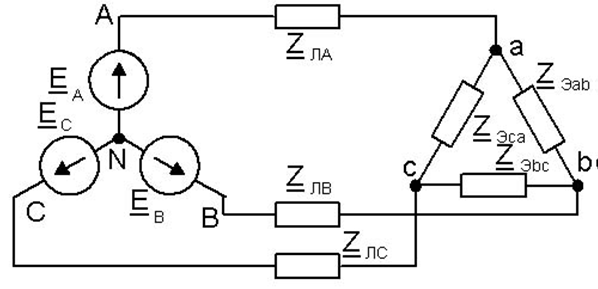
Рисунок 7 – Преобразование нагрузки в треугольник
16 Сопротивления фаз звезды эквивалентной нагрузки
|
ZЭa=ZЭb=ZЭc=ZЭаbZЭcа/(ZЭаb+ZЭbc+ZЭcа)=(90-12,8571j)(90-12,8571j)/[(90- -12,8571j)+( 90-12,8571j) +(90-12,8571j)]= 30-4,2857j Ом; |
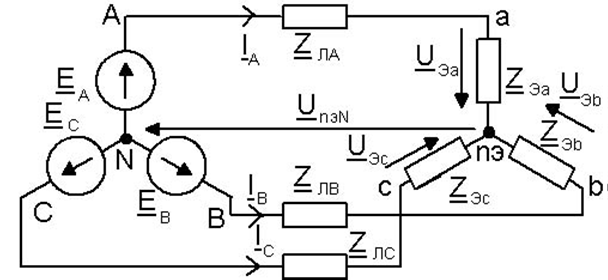
Рисунок 8 – Преобразование нагрузки в звезду
17 Сопротивления фаз системы
|
ZА=ZЛА+ZЭa=(26,4j)+( 30-4,2857j)= 30+22,1143j Ом; |
ZB=ZЛB+ZЭb=(-22j)+( 30-4,2857j)= 30-26,2857j Ом;
ZC=ZЛC+ZЭc=(26,4j)+( 30-4,2857j)= 30+22,1143j Ом.
18 Напряжение между нейтралями генератора N и эквивалентной звезды nэ
UnэN=(UA/ZА+UB/ZB+UC/ZC)/(1/ZА+1/ZB+1/ZC)=[(110/(30+22,1143j)+110e-j120/(30-26,2857j)+110ej120/(30+22,1143j)]/(1/(30+22,1143j)+1/(30-26,2857j)+1/(30 + +22,1143j))= 54,9470-10,9830j B.
19 Линейные токи генератора
IA=(UA-UnэN)/ZА=[110-(54,9470-10,9830j)]/( 30+22,1143j)= 1,3639-0,6393j A;
IB=(UB-UnэN)/ZB=[110 e-j120-(54,9470-10,9830j)]/(30-26,2857j)= -0,6808-3,4058j A;
IC=(UC-UnэN)/ZC=[110ej120-(54,9470-10,9830j)]/(30+22,1143j)=-0,6831+4,0451j A.
20 Падения напряжения в линиях
ΔUЛА=IA*ZЛА=(1,3639-0,6393j)( 26,4j)= 16,8766+36,0062j B;
ΔUЛВ=IB*ZЛB=(-0,6808-3,4058j)(-22j)=-74,9277+14,9768jB;
ΔUЛС=IC*ZЛC=(-0,6831+4,0451j)( 26,4j)= -106,7899-18,0339j B.
21 Фазные напряжения эквивалентной нагрузки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.