Расчет трехфазной цепи. Расчет симметричного режима трехфазной цепи, страница 7

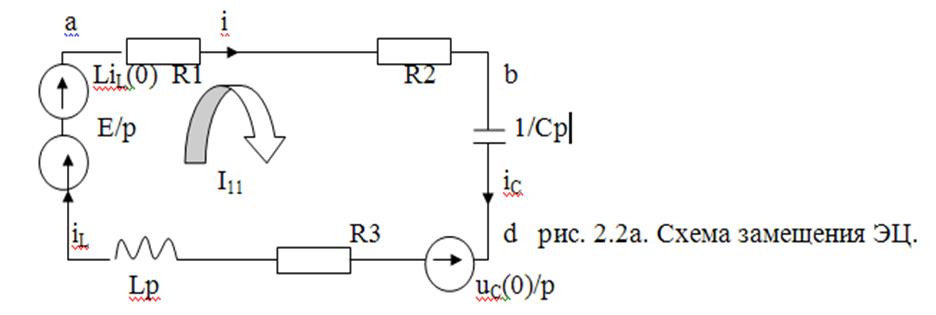
8.3 Операторные токи и напряженияв области действительного переменного р рассчи­тываются по тем же законам и теми же методами, что и в электрических цепях в области действительного переменного t . Согласно методу контурных токов из рис. 2.2аследует, что

I₁₁ (p)Z₁₁(p)  = E(p)                                                                                           (2.3а)

Где  Z₁₁ (p)= (R1+ R2+ R3)+1/Cp+ Lp                                                                     (2.4а) E(p)=E/p+ Li_L(0)  - u_C(0)/p                                                                              (2.5а)

Получаем:

I₁₁(p)=I_L(p)= I_C(p)=(E/p+Li_L(0)-u_C(0)/p )/(R1+R2+R3+1/Cp+Lp)                        (2.6а)

Решением уравнения (2.6а) будет контурный опера­торный ток, который нужно преобразовать к виду дробно-рациональной функции.

I₁₁(p)=I_L(p)= I_C(p)=(E+LI_L(0)p-u_C(0))C/(LCp²+( R1+R2+R3)Сp+1)=F_1L(p)/F_2L(p) =(100+0,001*4,545455*p-9,090909)*0,000005/ (0.001*0,000005*p²+ (20+15+5)* *5*10^-6p+1)=(0,000454545+2,27273E-08*p)/ (0,000000005p²+2*10^-4p+1) (2.7а) Операторное напряжение на конденсаторе, равное по закону Ома произведению опера­торных тока I_C (p) и сопротивления 1/Ср, также должно быть представлено дробно-рацио­нальной функцией

U_C(p)=I_C(p)/Ср+u_C(0)/p=(E+LI_L(0)p-u_C(0))/(LCp²+(R1+R2+R3)p+1)p+ u_C(0)/p =F_1C(p)/pF_2C(p)=[LCu_C(0)p²+(LI_L(0)+(R1+R2+R3)Cu_C(0))p+E]/[p(LCp²+(R1+R2+R3)Сp+1]=[10^-3*5*10^-6*9,090909p²+(10^-3*4,545455+(20+15+5)*5*10^-6* *9,090909) p+100]/[p(p*10^-3*5*10^-6 * p²+ (20+15+5)* 5*10^-6p+1)]=  [45,45455* *10^-9 +(4,545455*10^-3+18,181818*10^-4)p+100]  / (p(5*10^-9p²+2*10^-4p+1)       (2.8а)

2.4 Полюсы операторных токов и напряжений (2.7а) и (2.8а) определяются при равен­стве нулю знаменателя дробно-линейной функции

F₃(p)=pF₂(p)= p(5*10^-9p²+40p+1)=0.                                                       (2.9a)                                                                        

Решение (2.9a) дает ро=0, p₁= p₁= -5857,86 с^-1: и p₂=- p₂= -34142,1с ^-1

Полюсы p₁и р₂ операторных тока I_L(p). и напряжения U_C(p) будут равны корням харак­теристического уравнения (2.12).

Нулевой полюс свидетельствует о наличии принужденной составляющей напряжения на конденсаторе  (2.8а).

Отсутствие нулевого полюса в токе через конденсатор и  индуктивность             (2.6а)  говорит о том, что имеет место только свободная составляющая.

          8.5 Нахождение оригинала по изображению осуществляется чаше всего по формулам разложения, основанным на теореме разложения. В случае действительных сопря­женных полюсов оригинал находится по формуле разложения

F(p) =F₁(_P)   =>    f(t) = F₁(p₁) e^p1t   +   F₁(p₂) e^p2t                                             (2.10a)                                                                                             

            F₂(p)                    F₂'(p₁)              F₂'(p₂)

Производная функции свободных составляющих F₂(p) знаменателя операторных токов F₂'(p) = 10^-8p + 2*10^-4.                                                  (2.11a)                                                                                              Переходный ток в индуктивности согласно (2.6a) и (2.7a)

i_L=> I_L(p)= (0,000454545+2,27273E-08*p)/ (0,000000005p²+2*10^-4p+1)=  =F_1L(_P)/F_2L(p)     =>[(0,000454545+2,27273E-08*(-5857,86)]/ [10^-8*(-5857,86) + +2*10^-4 ]*e^-5857,86t + [(0,000454545+2,27273E-08*(-34142,1)]/ [10^-8*(-34142,1) + +2*10^-4 ]*e^-34142,1t=2,272727818*e^-5857,86t +2,272727818*e^-34142,1t                             (2.12a)                                                                                              Переходное напряжение на конденсаторе . В случае нулевого и действи-тельных сопря­женных полюсов оригинал находится по формуле разложения

F(p) = F₁(_P)   =>    f(t) =F₁(0)   + F₁(p₁) e^p1t   +   F₁(p₂) e^p2t                                             (2.13a)                                                                                             

           pF₂(p)                  F₂(0)      p₁ F₂'(p₁)            p₂  F₂'(p₂)