Машиностроение \ Конструирование и проектирование транспортных машин

Механизация транспортирования угля по бремсбергу на базе конвейера 2Л100У, страница 13

[σ]Н=664,65 МПа – допустимое напряжение;  

 jа=0,315 - коэффициент межосевого расстояния

     ,   Н∙м

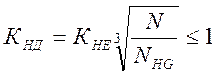
NHG = ( НВ )3=3003=2,7∙107 - базовое число циклов нагружения;         

N = 60∙n1∙nз∙t=60∙54,28∙1∙18000=5,68∙107 - число циклов нагружения;            

КНД – коэффициент долговечности;

КНЕ = 0,63 – коэффициент эквивалентности;

n3 – число зацеплений колеса;

 t = 18000 - время работы колеса, ч.

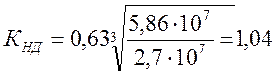
Принимаем КНД = 1.

 (Н∙м);

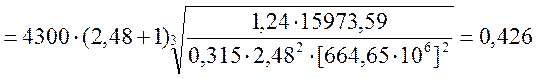аW (м).

Округляем до стандартного значения аW  =0,425 м

2.4.10.2. Предварительные основные размеры колеса

Делительный диаметр:

Ширина:

,

Округляем до стандартного значения =130 мм.

2.4.10.3. Модуль передачи

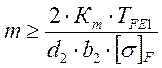,   м

где Кm =5,8 – для косозубых колес;

[σ]F – допустимое напряжение, Мпа;

ТFE1 – эквивалентный момент на колесе,Н∙м;

ТFE1 = КFД  ∙Т1

КFД – коэффициент долговечности;

 При  N>108 ,KFД = 1 (N=1,454∙108)

ТFE1 = 1∙15973,59 = 15973,59 (Н∙м);

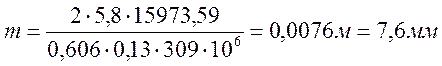
Полученное значение модуля округляем в большую сторону до стандартной величины: m = 8 мм

2.4.10.4. Число зубьев и угол наклона

Угол наклона зубьев:

βmin = arcsin(3,5×m/b2)= arcsin(3,5×0,008/0,13)=12,440

Суммарное число зубьев

   Полученное значение округляем в меньшую сторону до целого числа.

=103;

Действительный угол наклона зубьев:

β = arccos(×m/(2×аW))= arccos(103×0,008/2×0,425)=14,21.

Число зубьев шестерни и колеса:

 

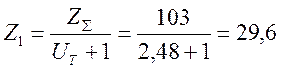
Принимаем  =30    

Число зубьев колеса:

,       

Фактическое передаточное число:

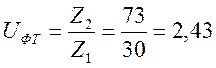
2.4.10.5. Геометрические размеры колеса и шестерни

Делительный диаметр шестерни:

Делительный диаметр колеса:

Диаметры окружностей вершин dа и впадин df зубьев:

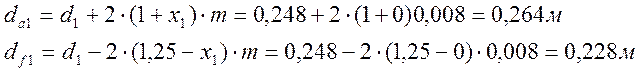
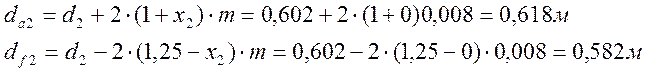
где X1=X2=0 – коэффициенты смещений.

2.4.10.6. Силы в зацеплении

Окружная сила:

2ּ15973,59/0,606=52718,1 Н

Радиальная сила:

Осевая сила:

2.4.10.7. Проверка зубьев по напряжениям изгиба

Расчетное напряжение изгиба в зьбьях колеса:

=309 МПа

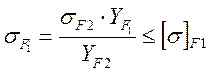=370  МПа  

где σF2 – напряжение изгиба для колеса,   Па;

КFa =1 – коэффициент угла зацепления принимаем по [5. с.14];

V=πd2nт/60=3,14∙0,606∙54,28/60=1,72 м/с – окружная скорость;

КFV = 1,07 – коэффициент динамической нагрузки принимаем по [5. табл. 2,7];

YF1 = 3,8 – коэффициент формы зуба шестерни принимаем по [5. табл. 2,8];

YF2 = 3,61 – коэффициент формы зуба колеса;

Коэффициент Yβ вычисляется по формуле:

Yβ=1 - β/140 = 1 -14,21/140= 0,899

FtE – эквивалентная окружная сила,   Н.

FtE = KFД∙Ft

 т.к. N=1,454∙108>108, принимаем KFД =1        

FtE = 1∙52718,1= 52718,1 (Н);

 

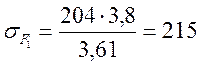 (МПа).

[σ]F1 = 370 МПа > σF1 = 215 МПа – условие выполняется.

[σ]F2 = 309 МПа > σF2 = 204 МПа – условие выполняется.

2.4.10.8. Проверка зубьев колес по контактным напряжениям

Расчетное контактное напряжение:

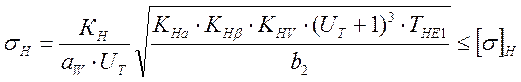,   МПа   

где КНа = 1,1 – для косозубых колес;

КН =270000 – для косозубых колес;

    КНV =1,03 – коэффициент динамической нагрузки принимаем по [5.табл. 2,9];

 

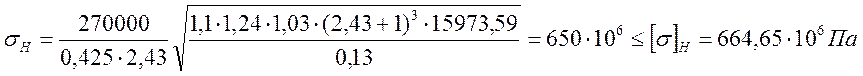
Условие выполняется.

2.4.11. Конструирование валов

Ведущий вал (№4):

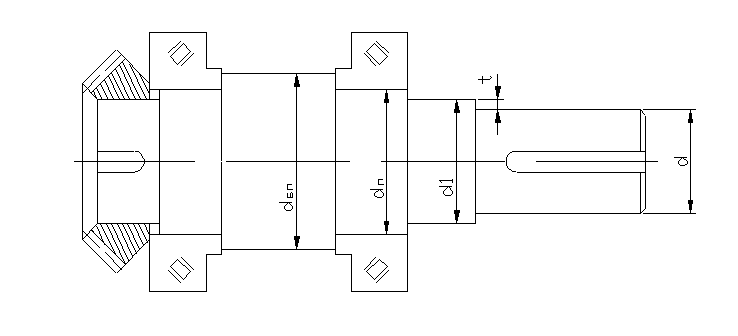
рис. 2.5 Ведущий вал.

Определяем диаметр ведущего вала:

,

Принимаем d  = 71 мм.

d1 = d + 2t= 71+2×3,5=78 мм;

Диаметр вала под подшипники:

dП ≥ d + 2×t = 71+2×3,3=77,6 мм;

Принимаем dП =80 мм.

Диаметр буртика под подшипники:

dБП ≥ dП+3r = 80+3×3,5=87 мм .

Промежуточный вал №3:

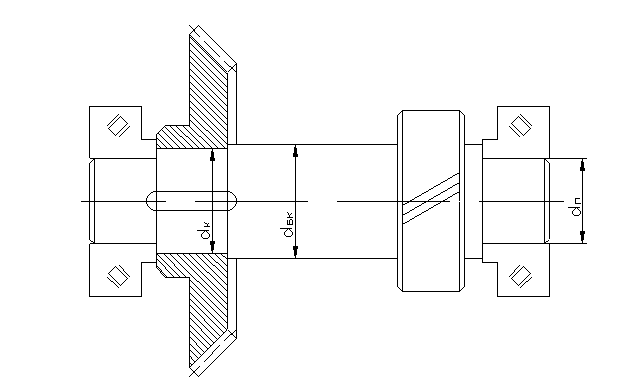
Рис. 2.6. Промежуточный вал №3

Диаметр вала под колесо:

Принимаем dк = 95 мм.

Диаметр буртика под колесо:

dБК ≥dк +3×f = 95+3×2,5= 102,5 мм

Диаметр вала под подшипники:

dП ≥ dk - 3×r = 95-3×34= 83 мм

Принимаем dП =90 мм.

Промежуточный вал №2:

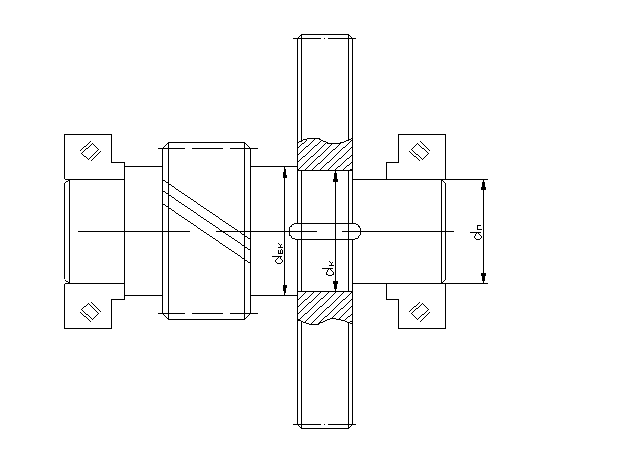
Рис. 2.7. Промежуточный вал №2:

Диаметр вала под колесо:

Принимаем dк = 120 мм.

Диаметр буртика под колесо:

dБК ≥dk + 3f =120+3×2,5=127,5мм

Диаметр под подшипники:

dП ≥ dk-3r = 120-3×4=108 мм

Принимаем dП =110 мм

  Ведомый вал №1:

Определяем диаметр ведомого вала:

,

Принимаем d = 140 мм.

Диаметр вала под подшипники:

dП ≥ d+2×t = 140+2×3,5 = 147мм;

Принимаем dП=150 мм.

Скачать файл