Механизация транспортирования угля по бремсбергу на базе конвейера 2Л100У, страница 12

Z_V1=Z₁/(cos³β_mcosδ₁)=26/(cos³35∙cos25)=52

Z_V2=Z₂/(cos³β_mcosδ₂)=26/(cos³35∙cos75)=654

Угол β_m =35⁰

    Y_F1 = 3,65;  Y_F2 = 3,6     

   F_tE – эквивалентная окружная сила, Н;

F_tE = K_FД∙F_t, Н;

где: K_FД – коэффициент долговечности, принимается = 1, т.к. N>10⁸;  

F_tE =1∙11760 = 11760H

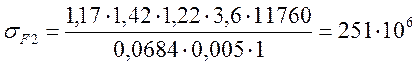Па<[σ]_F2=309Мпа;

σ_F1=251×3,65/3,6=254Мпа<[σ]_F1=370Мпа.

2.4.8.8. Проверка зубьев колес по контактным напряжениям

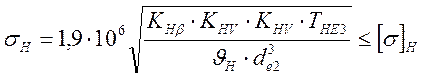
где: К_НV =1,07 – коэффициент динамической нагрузки принимается по [5. табл.2,9]

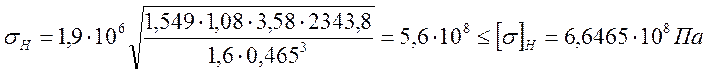
2.4.9. Расчет промежуточной ступени

2.4.9.1 Межосевое расстояние

а_W 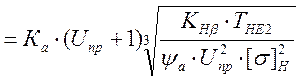,   м   

где К_а = 4300 – коэффициент для косозубых колес

К_Нβ – коэффициент концентрации нагрузки

К_Нβ= К⁰_Hβ – для неприрабатывающихся колес

Коэффициент К⁰_Hβ  принимается по [5. табл. 2,3] в зависимости от коэффициента Ψ_d :

Ψ_d= 0,5Ψ_a (U_пр+1)=0,5∙0,315(2,98+1)=0,63

Ψ_а=0,315 - коэффициент межосевого расстояния

К⁰_Hβ=1,24 (при НВ≤350, схема №6)

Т_НЕ2 – эквивалентный момент на колесе,   Н∙м;    

, Н∙м

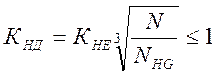
N_HG = ( НВ )³=300³=2,7∙10⁷

N = 60∙n₂∙n_з∙t = 60∙134,61∙1∙18000=1,454∙10⁸

 

 

где К_НД – коэффициент долговечности;

 К_НЕ = 0,63 – коэффициент эквивалентности;

 N_HG – базовое число циклов нагружения;

 N – число циклов нагружения;

 n_з – число зацеплений колеса;

 t = 18000 - время работы колеса,   ч.

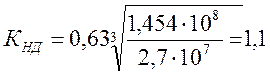
Принимаем К_НД = 1

                    (Н∙м);

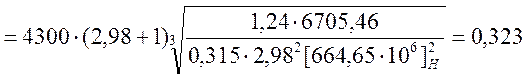     а_W (м).

Так как данное межосевое расстояние не позволяет разместить колесо быстроходной ступени на валу №3, то принимаем а_W  =400 мм

2.4.9.2. Предварительные основные размеры колеса

Делительный диаметр:

Ширина:

2.4.9.3. Модуль передачи

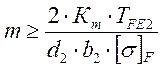,  м

где К_m =5,8 – для косозубых колес;

Т_FE2 – эквивалентный момент на колесе (вал №2),   Н∙м;

 [σ]_F – допустимое напряжение (меньшее из двух значений [σ]_F1и [σ]_F2), МПа.

Т_FE2 = К_FД ∙Т₂

К_FД = К_FE

При N≥10⁸ (N=1,454∙10⁸ )коэффициент К_FД =1

Т_FE2 = 1∙6705,46= 6705,46 (Н∙м);

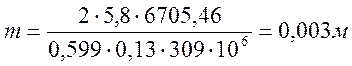
Так как вычисленное значение модуля слишком мало, принимаем m = 6 мм.

2.4.9.4. Число зубьев и угол наклона

Минимальный угол наклона зубьев:

β_min = arcsin(3,5m/b₂)= arccos(3,5×0,006/0,13)=9,3⁰.

Суммарное число зубьев:

    Полученное значение округляем в меньшую сторону до целого числа.

=131;

Действительный угол наклона зубьев:

β = arccos(×m/(2×а_W))= arccos(131×0,006/(2×0,4))=10,73⁰.

   Число зубьев шестерни:

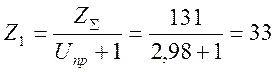
Число зубьев колеса:

 

Фактическое передаточное число:

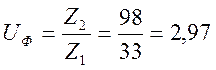
2.4.9.5. Геометрические размеры колеса и шестерни

Делительный диаметр шестерни:

Делительный диаметр колеса:

Диаметры окружностей вершин d_а и впадин d_f зубьев:

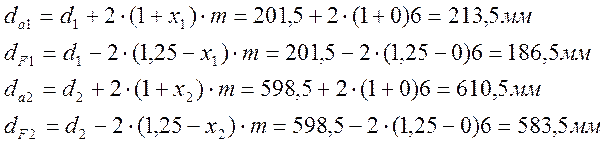
где х₁ = х₂=0 – коэффициенты смещений у шестерни и колеса.

2.4.9.6. Силы в зацеплении

Окружная сила:

2ּ6705,46/0,5985=22407,6 Н

Радиальная сила:

Осевая сила:

2.4.9.7. Проверка зубьев по напряжениям изгиба

Расчетное напряжение изкгиба в зубьях колеса:

=309,   МПа

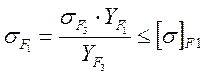=370,   МПа            

где σ_F – напряжение изгиба,  Па;

К_Fa =1 – коэффициент угла зацепления;

Коэффициент К_Fβ= К_Fβ⁰=1,16 принимается по [5.табл.2,6]

К_FV = 1,14 – коэффициент динамической нагрузки принимается по [5.табл.2,7];

Коэффициент Y_β вычисляется по формуле:

Y_β= 1 - β/140= 1-9,3/140= 0,934

Y_F1 = 3,8 – коэффициент формы зуба шестерни принимается по [5.табл.2,8];

Y_F2 = 3,6 – коэффициент формы зуба колеса;

F_tE – эквивалентная окружная сила,   Н.

F_tE = K_FД∙F_t=1ּ22407,6=22407,6   Н

 

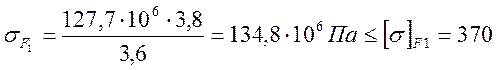 МПа.

Условия выполняются.

2.4.9.8. Проверка зубьев колес по контактным напряжениям

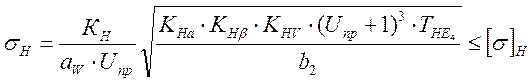,   МПа  

где К_На = 1,1 – для косозубых колес;

      К_Н =270000 – для косозубых колес;

      К_НV =1,05 – коэффициент динамической нагрузки принимается по [5.табл.2,9];

 

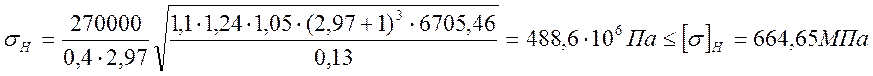
Условие выполняется.

2.4.10. Расчет тихоходной ступени

2.4.10.1. Межосевое расстояние

Межосевое расстояние:

а_W 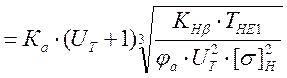,   м     

где К_а = 4300 – коэффициент для косозубых колес;

К_Нβ = К_Нβ⁰ =1,24 коэффициент концентрации нагрузки принимается по [5.таб.2,6];

Т_НЕ1 – эквивалентный момент на колесе (вал №1),   Н∙м;