Машиностроение \ Конструирование и проектирование транспортных машин

Механизация транспортирования угля по бремсбергу на базе конвейера 2Л100У, страница 11

Принимаем следующий вариант термообработки:

т.о. колес – улучшение, твердость НВ 269…302; т.о. шестерен – улучшение и   закалка ТВЧ, твердость поверхности HRC 48…53. Марки сталей одинаковы для колес и шестерен – Сталь 40ХН.

        Допускаемые контактные напряжения [5, табл.2.1]:

* Индекс «1» здесь и в дальнейшем относится к шестерне, индекс «2» - к колесу.

        Допускаемые напряжения изгиба[5, табл.2.1]:

        Расчетное допускаемое контактное напряжение:

Должно выполнится условие:  

664,65<1,15∙607=698,05 (условие выполняется)

2.4.8. Расчет конической быстроходной ступени

2.4.8.1. Диаметр внешней делительной окружности колес

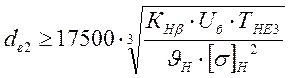
где: коэффициент КНβ для неприрабатывающихся колес с круговым зубом равен:

- коэффициент концентрации нагрузки принимают по [5, табл. 2,3] в зависимости от коэффициента ψd  и схемы передачи:

=2,4 (схема №2, НВ≤350)

 [σ]Н =664,65 МПа – расчетное допустимое контактное напряжение;

 Коэффициент для колес с круговым зубом принимают:

ТНЕ3 – эквивалентный момент на колесе (вал №3), Н∙м;

,Н∙м

где: КНД – коэффициент долговечности;

,

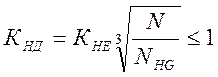где: КНЕ = 0,63 – коэффициент долговечности, зависящий от режима нагружения;

      NHG – базовое число циклов нагружения;

      N – число циклов нагружения;

    NHG = ( НВ )3 = (300)3 = 27000000;

N = 60∙n∙nз∙t,

где: nз – число зацеплений колеса;

        t = 18000 - время работы колеса, ч.

        n – частота вращения колеса (вал №3);

N = 60∙401,14∙1∙18000 = 43323×104;

Принимаем КНД = 1, тогда ТНЕ3=Т3.

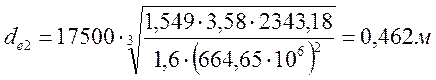
2.4.8.2. Конусное расстояние и ширина колес

Угол делительного конуса колеса и шестерни:

δ2= arctg Uб = arctg 3,58 = 74,390

  Принимаем ближайший больший угол δ2 = 750

Конусное расстояние:

Rе= dе2/(2× sin δ2)=0,462/(2×sin750)=0,24 м

Ширина колёс.

b = 0,285×Rе =0,285×0,24 = 0,0684 м=68,4 мм

2.4.8.3. Модуль передачи

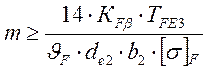
где: Коэффициент  для колес с круговым зубом принимают:

   ТFE3 – эквивалентный момент на колесе, Н∙м;

   [σ]F – допустимое напряжение на изгиб (меньшее из значений [σ]F1 и [σ]F2), Па.

Коэффициент    

 принимается из [5. табл.2,6] для ψd=0,617, НВ≤350, схема №2

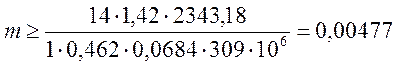м =4,77мм

Округляем до стандартной величины m = 5мм.

2.4.8.4. Число зубьев колеса и шестерни

Число зубьев колеса:

Z2= е2/m = 0,462/0,005=92,4

Принимаем Z2 =93.

Число зубьев шестерни:

Z1= Z2 / Uб =93/3,58=26

Фактическое передаточное число:

Uф= Z2 /Z1 =93/26 = 3,58.

2.4.8.5. Геометрические размеры колеса и шестерни

Углы делительных конусов колеса и шестерни:

δ2= arctg Uб = arctg 3,58 = 74,390

  Принимаем ближайший больший угол δ2 = 750

δ1=90 -  δ2=90 - 75 = 250

Делительный диаметр шестерни:

de1= Z1×m =26 × 5 = 130 мм

Делительный диаметр колеса:

de2= Z2×m =93 × 5 = 465 мм

Внешние диаметры колёс:

dea1 = de1 +1,64(1+Xn1) ×m×cos δ1 =130+1,64×(1+0,25)×5×cos250 = 139,9мм

dea2 = de2 +1,64×(1+Xn2) ×m×cos δ2= 465+1,64×(1+ 0,25)×5×cos750 = 466,6мм

где  Xn1 и Xn2 - коэффициенты смещения принимаются по [5. табл. 2,11].

2.4.8.6. Силы в зацеплении

Окружная сила на среднем диаметре колеса:

Ft = 2×T3/ dm2 = 2×2343,18/0,3985 = 11760Н;

где: dm2 =0,857×de2 =0,857×465 = 0,3985 м

Радиальная сила на шестерне:

Fr1 = γr×Ft  = 0,103×11760 = 1211,28Н;

Осевая сила на шестерне:

Fа = γа×Fт= 0,82×11760 = 9643,2 Н.

где коэффициенты γr и γа определяются как:

γr=0,44cos δ1 - 0,7sin δ1=0,44cos25 - 0,7sin25 = 0,103

γа=0,44sin δ1 + 0,7cos δ1=0,44sin25 + 0,7cos25 =0,820

2.4.8.7. Проверка зубьев по напряжениям изгиба

Расчётное напряжение изгиба в зубьях колеса:

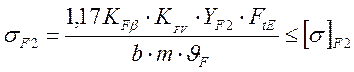
Напряжение изгиба в зубьях шестерни:

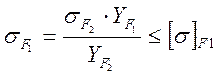= 370 МПа,

где σF2 –напряжение изгиба для колеса, MПа;

КFV = 1,22 – коэффициент динамической нагрузки принимается по [5. табл.2,7] при окружной скорости на среднем диаметре колеса равной:

V = p∙ dm2∙ n3 /60=3,14∙0,3985∙401,14/60=8,4 м/с

Значения коэффициентов YF1  и  YF2 принимают по [5. табл.2,8] по эквивалентным числам зубьев:

Скачать файл