Схемотехника: Лабораторный практикум, страница 2

Лабораторная работа №1

ИССЛЕДОВАНИЕ ПАССИВНЫХ RC-ФИЛЬТРОВ

Цели работы – изучение свойств RC-фильтров низких и высоких частот, а также полосовых фильтров, приобретение навыков работы с генератором сигналов специальной формы и цифровым осциллографом.

1.1. Основные теоретические сведения

Простейшими элементами электронных схем являются двухполюсники. Различают пассивные и активные двухполюсники. Активные двухполюсники являются источниками энергии, например, источники тока и напряжения.  Вольтамперная характеристика пассивного двухполюсника всегда проходит через начало координат вольтамперной характеристики. Пассивные двухполюсники бывают линейными и нелинейными. Примером нелинейного двухполюсника является полупроводниковый диод. Резисторы, конденсаторы и индуктивности относятся к линейным двухполюсникам – их вольтамперные характеристики представляют собой прямую линию, рис. 1.1.

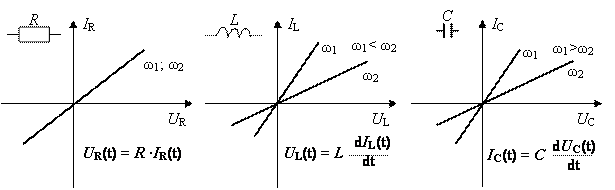
Рис. 1.1. Вольтамперные характеристики линейных двухполюсников

Вольтамперная характеристика не отражает фазовых соотношений между током и напряжением на двухполюснике. Кроме этого из приведенных линейных зависимостей видно, что индуктивное и емкостное сопротивления зависят от частоты. Зависимость фазы и модуля полного сопротивления электрическому току Z рассматриваемых двухполюсников от угловой частоты ω прикладываемого синусоидального напряжения приведены на рис. 1.2.

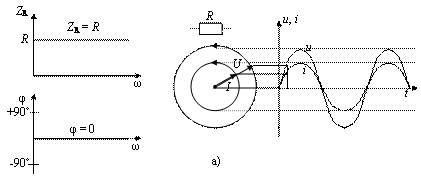
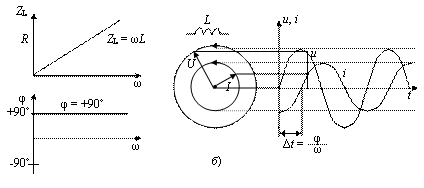
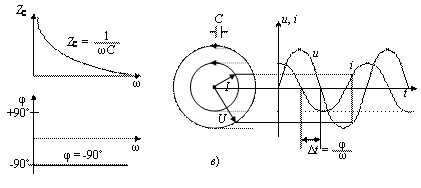
Рис. 1.2. Зависимость модуля импеданса Z, фазового сдвига φ между током и

напряжением, векторная диаграмма Френеля и осциллограммы тока

и напряжения на резисторе (а), индуктивности (б) и конденсаторе (в)

Если собрать делитель напряжения из пары пассивных двухполюсников разного типа, например из резистора и конденсатора, то возникает цепь, попадающая под понятие пассивный четырехполюсник, рис. 1.3.

Очевидно, что выходное напряжение U₂(t) на рис. 1.3 а) и б) должно зависеть от частоты входного напряжения U₁(t) в результате изменения емкостного сопротивления конденсатора. Фаза выходного напряжения при изменении частоты также не останется неизменной, т. к. вклад в полное сопротивление цепи со стороны компонента (конденсатора), у которого имеется фазовый сдвиг между током и напряжением будет разным для разных частот.

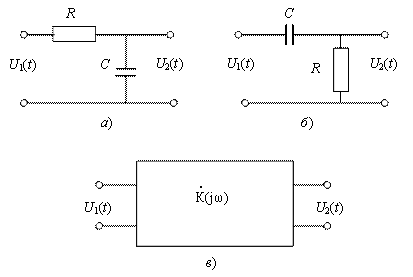
    Рис. 1.3. Четырехполюсники: фильтр нижних частот (а), фильтр верхних

                                частот (б) и обобщенное изображение четырехполюсника (в)

Итак, если на входе условного четырехполюсника действует гармонический сигнал с зависимой от частоты фазой:

,

то в результате линейности элементов, образующих четырехполюсник,  выходной сигнал останется синусоидальным, но будет иметь другую амплитуду и дополнительный, зависимый от частоты, фазовый сдвиг:

.

Комплексная передаточная функция, учитывающая амплитудные и фазовые соотношения между входным и выходным сигналами, имеет вид:

                                               (1.1)

Данная функция всегда может быть приведена к виду:

,                                                   (1.2)

где K(ω) – модуль комплексного числа.