Анализ и синтез на базе комплекса технических средств гипотетической микропроцессорной системы оптимального управления технологическим процессом и оборудованием технического объекта (Парогенератор), страница 4

Суть алгоритма состоит в поддержании на выходе Y2 значения, максимально близкого к заданному (Y2*) с помощью регулирования управляемых переменных U1 и U2.

5.2. Оценка эффективности управления по предложенному алгоритму

С целью оценки эффективности управления по предложенному алгоритму поставим следующий эксперимент: дважды произведем реализацию информационного режима при нормальной эксплуатации  и при осуществлении ручного управления по предложенному алгоритму. Для каждого случая оценим выбранный критерий оптимальности управления. Если его значение при осуществлении ручного управления окажется меньше, чем в режиме нормальной эксплуатации, то можно говорить об эффективности управления по предложенному алгоритму.

Снятие данных в режиме нормальной эксплуатации при фиксированных управляемых переменных (U1 и U2) (данные peregrev.i10):

Рис. 39. Расчет ТЭП 1 при нормальной эксплуатации.

Рис. 40. Расчет ТЭП 2 при нормальной эксплуатации.

Снятие данных в режиме нормальной эксплуатации при осуществлении ручного управления по предложенному алгоритму рис. 10 (Y2* = 6) (данные peregrev.i11):

Рис. 41. Расчет ТЭП 1 при осуществлении ручного управления.

Рис. 42. Расчет ТЭП 2 при осуществлении ручного управления.

Из приведенных данных видно, что ручное управление оказалось более эффективным, т.к. значение ТЭП 2 (дисперсии Y2) уменьшилось на порядок и выбранное значение выходной переменной может быть поддержано с большей точностью.

5.3. Оценивание интервалов корреляции

Для того, чтобы сделать обоснованные суждения о виде и характере возмущений в исследуемом ТОУ, выбрать оптимальные интервалы съема данных и т.п. нам потребуются сведения об интервалах корреляции.

Произведем анализ данных, снятых в режиме нормальной эксплуатации при фиксированных управляемых переменных (U1 и U2) (данные peregrev.i12):

Рис. 43. Расчет средних значений X1 и X2.

Рис. 44. Расчет числа пересечений реализацией X1(t) линии, соответствующей среднему значению процесса.

Рис. 45. Расчет числа пересечений реализацией X2(t) линии, соответствующей среднему значению процесса.

Интервал корреляции (время затухания автокорреляционной функции случайного процесса) может быть грубо оценен через соотношение:

,

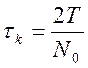где N₀ – число пересечений реализацией x(t) за T время линии, соответствующей среднему значению процесса.

Для X1: N₀₁=25, 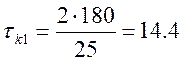c

Для X2: N₀₂=19, 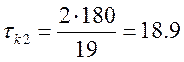c

Число ординат автокорреляционных функций n = 10.

Интервал дискретизации съема данных для вычисления n ординат автокорреляционной функции может быть оценен с помощью соотношения: .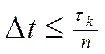

с; с.

5.4. Уточнение интервалов корреляции

Выберем в качестве интервала дискретизации  и произведем снятие данных (данные peregrev.i13). По полученным данным построим авто- и взаимнокорреляционные  функции и произведем уточнение интервала корреляции.

Рис. 46. График автокорреляционных функций.

Рис. 47. График взаимнокорреляционной функций.

Уточненные значения интервалов корреляции могут быть вычислены с использованием следующего соотношения:

, где  - интервал дискретизации, n – количество ординат автокорреляционной функции, за которые она затухает.

с; с

Выберем в качестве интервала дискретизации  и произведем повторное снятие данных (данные peregrev.i14) с уточнением интервала корреляции:

Рис. 48. График автокорреляционных функций.

Рис. 49. График взаимнокорреляционной функций.

Уточненные значения интервалов корреляции:

с; с

5.5. Построение регрессионной модели

Для математического описания и получения статических характеристик ТОУ, выходная переменная которого зависит от многих входных переменных, наиболее совершенными являются экспериментально-статистические методы. Аппарат корреляционного и регрессионного анализов позволяет получить математическое описание объекта в виде полинома заданного вида, связывающего входные и выходные переменные в статическом режиме. Полученная зависимость называется уравнением регрессии.

С целью накопления исходного статистического материала поставим пассивный эксперимент. Он основан на регистрации контролируемых параметров процесса в режиме нормальной эксплуатации работы объекта без внесения преднамеренных возмущений. Для увеличения точности регрессионной модели необходимо оптимальным образом выбрать интервал съема данных . В частности, если при любых интервалах корреляции взаимная ковариация между переменными отсутствует, оптимальный выбор должен производиться из условия , j=1,k, где  - интервал корреляции (время затухания) процесса X_j(t). т.е интервал  между соседними отсчетами должен, быть (больше чем время затухания автокорреляционной функции самого "медленного" случайного процесса. В этом случае величины выборочной дисперсии стремятся к 0, что ведет к увеличению объема доверительной области, которая с заданной вероятностью накрывает неизвестные истинные значения коэффициентов, входящих в уравнение регрессии. Однако не имеет смысла делать  много больше времени , т.к. при этом продолжительность эксперимента  существенно возрастает, а величины выборочных дисперсий практически не меняются.

Для оценки работоспособности полученной регрессионной модели часто вычисляют множественный коэффициент корреляции (характеризует тесноту связи между входными и выходной переменной), т е анализируют разность между единицей и величиной отношения дисперсии внешнего шума к выборочной дисперсии выходной переменной, рассчитанной относительно своего среднего значения. Можно считать регрессионную модель достаточно точной, если множественный коэффициент корреляции более 0.86.

В моменты времени t₁, t₂,..., t_n, разделенные ин­тервалом  будем измерять значения входных переменных X1, X2, U1, U2 и выходных пе­ременных Y1, Y2. Полученные данные будем использовать для нахождения оце­нок регрессионной модели и оценки дисперсии внешнего шума.