Закон изменения тока короткого замыкания зависит от расположения точки короткого замыкания (КЗ). КЗ вблизи синхронных генераторов в первый момент приводит к появлению ряда апериодических составляющих, затухающих со временем. КЗ в сетях, обладающих значительной емкостью (номинальное напряжение более 220 кВ) приводит к появлению заметных гармонических свободных составляющих. КЗ вблизи мощных нагрузок с большой долей синхронных или асинхронных двигателей вызывает дополнительные апериодические составляющие. В практических расчетах, направленных на выбор и проверку оборудования, не выясняют закон изменения ТКЗ и ограничиваются определением тока для начального момента времени (сверхпереходный ток), в некоторых случаях приближенно учитывают апериодические составляющие (ударный ток и его действующее значение).
2.1. ПЕРЕХОДНЫЙ ПРОЦЕСС В ПРОСТЕЙШЕЙ ЦЕПИ.
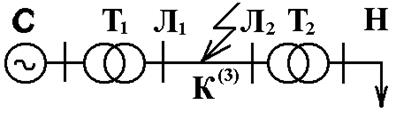
Рассмотрим процесс трехфазного КЗ в электрической сети номинального напряжения менее 220 кВ, будем считать, что точка КЗ значительно удалена как от генераторов, так и от потребителей (рис.2.1а). В этих условиях свободные составляющие ТКЗ, обусловленные влиянием генераторов, нагрузок и емкостных проводимостей сети, практически не проявляются.
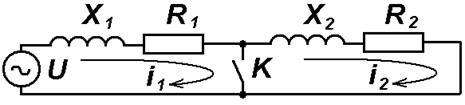
Рассматриваемая система состоит из питающей системы С, трансформаторов Т1,Т2, линии Л и нагрузки Н. В схеме замещения рис.2.1б. в соответствии с допущениями главы 1 не учитывается емкостная проводимость линии и потери холостого хода трансформаторов, нагрузка в силу удаленности от точки короткого замыкания учитывается приближенно активным и индуктивным сопротивлением. После эквивалентирования сопротивлений слева и справа от точки короткого замыкания схема замещения содержит два участка с параметрами X1,R1 и X2,R2, переходный процесс возникает при замыкании контакта К.
|
а |
б |
Рис.2.1. Принципиальная схема электрической сети и схема электрической цепи.
Расчет процесса трехфазного КЗ возможен как классическим, так и операторным методом. Рассмотрим оба метода.
2.1.1. Решение задачи классическим методом [4].
Для определения параметров переходного режима необходимо составить дифференциальные уравнения и найти их полные решения. Решение линейного дифференциального уравнения представляет собой сумму частного решения неоднородного уравнения и решения однородного уравнения.
Неоднородное уравнение цепи содержит заданные ЭДС или напряжения; частное решение его i′(t) является током установившегося режима. В однородном уравнении заданные ЭДС или напряжения равны нулю, ток i″(t) в цепи без источников затухает и называется свободным током. Полный ток
i(t) = i′(t) + i″(t).
Для сложной схемы дифференциальные уравнения составляют, например, в соответствии с первым и вторым законами Кирхгофа. Последовательным исключением неизвестных получают одно дифференциальное уравнение, в котором содержатся только неизвестное (искомый ток) и его производные:
a0dni/dtn + a1dn-1i/dtn-1 + …+ an-2d2i/dt2 +an-1di/dt + ani = f(t),
где f(t) содержит заданные ЭДС.
Для определения решения i″(t) однородного уравнения необходимо найти корни характеристического уравнения:
a0pn + a1pn-1 + …+ an-2p2 +an-1p + an = 0.
При простых корнях:
i″(t) = A1ep1t +A2ep2t + …+ Anepnt.
Корни характеристического уравнения могут быть также кратными и комплексными (попарно сопряженными). При кратных (повторяющихся) корнях в решении появляются экспоненты, помноженные на t(k-1), где k – кратность корня. Попарно сопряженным комплексным корням соответствуют гармонические составляющие в решении. Постоянные интегрирования Ak определяются из физических начальных условий.
Составление дифференциальных уравнений.
Составим дифференциальное уравнение по рис.2.1б для участка цепи с параметрами X1,R1 после замыкания контакта K. По второму закону Кирхгофа сумма падений напряжений в замкнутом контуре равна сумме приложенных ЭДС (напряжений). Для цепи переменного тока:
U = UR1 + UX1, или:
|
U = i1R1 + L1di1/dt. |
(2.1) |
После короткого замыкания, замыкания контакта K по рис. 2.1б, участок цепи с параметрами X2,R2 теряет связь с источником питания, к нему приложено нулевое напряжение. Для участка цепи с параметрами X2,R2 после замыкания контакта K:
0 = UR2 + UX2, или:
|
0 = i2R2 + L2di2/dt. |
(2.2) |
Определение тока установившегося режима.
Частное решение неоднородного
уравнения для участка цепи с параметрами X1,R1 является током установившегося режима контура с
сопротивлением Z1 = R1 + jX1 = Z1℮jφ1,гдеZ1 =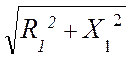 
, φ1 = arctg(X1/R1):
I′1 = U/ Z1.
Если записать приложенное к контуру напряжение в виде Umsin(ωt + α), то
i′1(t) = I1msin (ωt + α – φ1), I1m = Um/.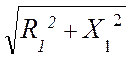
Частное решение неоднородного уравнения для участка цепи с параметрами X2,R2 равно нулю, поскольку после замыкания контакта к нему приложено нулевое напряжение.
Составление и решение однородного уравнения.
Однородное уравнение для участка цепи с параметрами X1,R1:
0 = UR1 + UX1, или:
0 = i1R1 + L1d i1/dt.
Характеристическое уравнение:
R1 + pL1 = 0.
Его решение:
p1 = - R1/L1.
Свободный ток участка цепи:
i″1(t) = A1e p1t.
Постоянную интегрирования A1 определим из условия непрерывности полного тока в цепи с индуктивностью: ток в цепи до коммутации, то есть до замыкания контакта K (t =0-):
i0 = Imsin(α – φ), где
Im = Um/√[(R1 + R2)2 + (X1 + X2)2], φ = arctg[(X1 +X2)/(R1 + R2)]
равен току в первый момент после коммутации при t = 0+
i1/0/= i′1/0/ + i″1/0/ = I1msin (α – φ1) + A1e0 .
Отсюда:
A1 = imsin (α – φ) – i1msin (α – φ1).
Однородное уравнение для участка цепи с параметрами X2,R2 после замыкания контакта:
0 = UR2 + UX2, или:
0 = i2R2 + L2d i2/dt.
Характеристическое уравнение:
R2 + pL2 = 0.
Его решение:
p2 = - R2/L2.
Свободный ток участка цепи:
i″2(t) = A2e p2t.
Постоянную интегрирования A2 определим из условия непрерывности полного тока в цепи с индуктивностью: ток в цепи до коммутации, то есть до замыкания контакта (t =0-)
i0 = imsin(α – φ)
равен току в первый момент после коммутации при t = 0+
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.