После подстановки (5) и (6) в (7) получим:
![]() =
=
![]() , (8), где ХΔL =
, (8), где ХΔL = ![]() (9)
(9)
Для тока прямой последовательности фазы А в месте разрыва имеем:
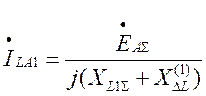 (10)
(10)
Зная все симметричные составляющие токов и напряжений, легко известным способом определить фазные величины токов и напряжений.
2 Обрыв двух фаз.
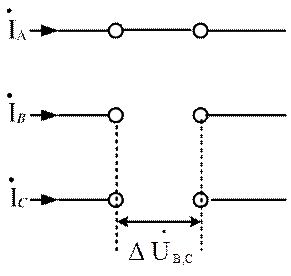 При разрыве двух фаз
(рис.3.33) граничные условия, очевидно, будут:
При разрыве двух фаз
(рис.3.33) граничные условия, очевидно, будут:
ILB = 0 (11)
ILC = 0 (12)
ΔULA = 0 (13)
Эти условия аналогичны граничным условиям однофазного короткого замыкания. В соответствии с
(11) и (12) следует, что симметричные составляющие
Рис. 3.33 тока фазы А в месте обрыва двух других фаз связаны простым соотношением:
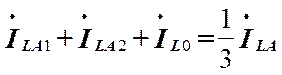 (14)
(14)
С другой стороны, поскольку согласно (13)
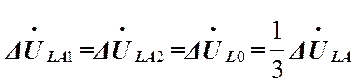 (15)
(15)
и учитывая (14), (19), получаем:
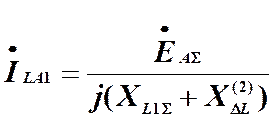 ,
(16)
,
(16)
где 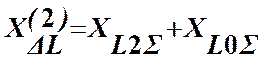 (17)
(17)
Для фазного тока согласно (14) имеем
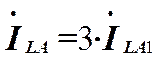 (18)
(18)
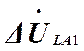 =
=
![]() -
- ![]() ·
· ![]() (19) Симметричные составляющие разности
(19) Симметричные составляющие разности
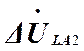 =
=
![]() -
- ![]() ·
· ![]() (20) фазных напряжений в
месте обрыва
(20) фазных напряжений в
месте обрыва
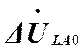 =
=
![]() -
- ![]() ·
· ![]() (21) определяются для обратной и
нулевой
(21) определяются для обратной и
нулевой
последовательностей
соответственно по (20) и (21), а для прямой последовательности проще по (15): 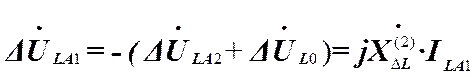 (22)
(22)
3.22 Для схемы Рис.3.34 определить токи и напряжения в линии и на шинах нагрузки при осуществлении неполнофазного режима (обрыв одной фазы).
![]()
![]()
![]()
![]()
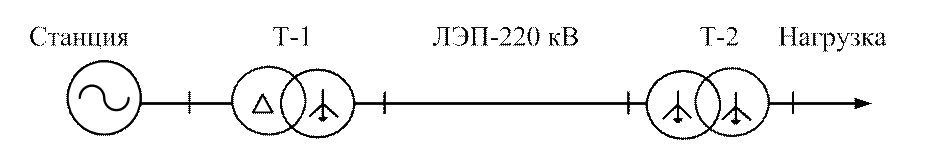
Рг = 240 МВт Sнт = 300 МВА l = 230 км Sнт = 300 МВА Uнагр = 115 кВ
Cos φ = 0,8 10,5/242 кВ Худ = 0,4 Ом/км 10,5/242 кВ Рн = 220 МВт
Uн = 10,5 кВ Uк = 14 % Uк = 14 % Cos φн = 0,98
Хd = 32%
Рис. 3.34
Решение
В соответствии с уравнением (4) составляем комплексную схему замещения (Рис.3.35)
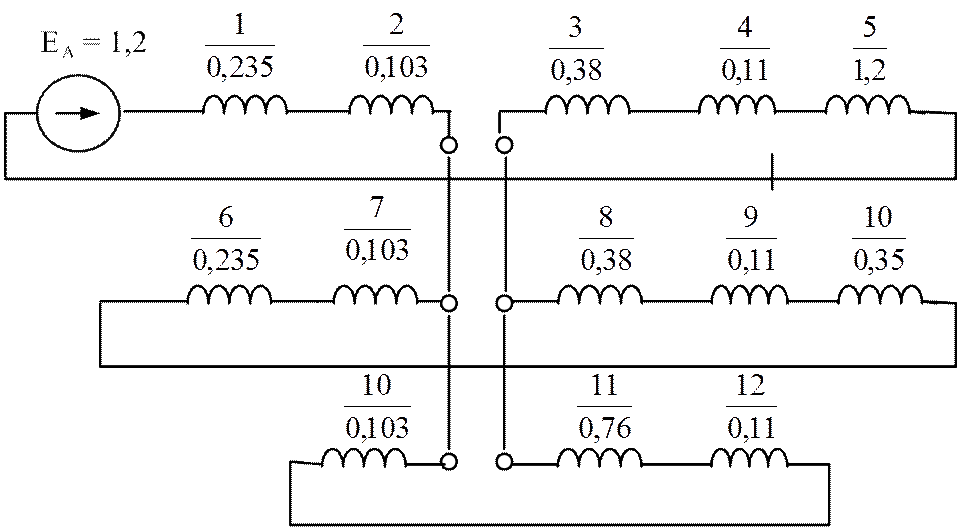
Рис. 3.35. Комплексная схема замещения
Расчет
ведем в относительных базисных единицах при ППОЕ. Принимаем базисные условия: Sб = 220 МВА; Uб = 115 кВ: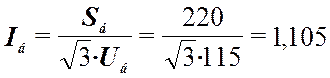 кА;
кА;
Рассчитываем сопротивления элементов схемы.
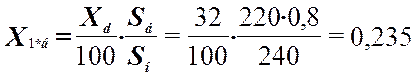 ;
; 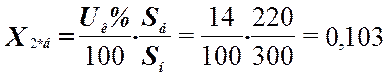 ;
;
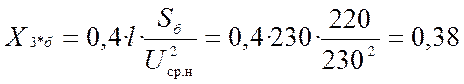 ;
; 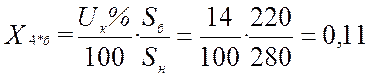 ;
;
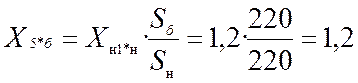 ;
; 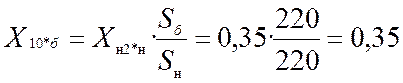 ;
;
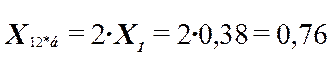 , т.к. линия с хорошо проводящими тросами.
, т.к. линия с хорошо проводящими тросами.
ХL1S = 0,38 + 0,11 + 1,2 + 0,235 + 0,103 = 2,028;
ХL2S = 0,38 + 0,11 + 0,35 + 0,235 + 0,103 = 1,178;
ХL0S = 0,76 + 0,11 + 0,103 = 0,973;
 .
.
Симметричные составляющие токов в месте обрыва:
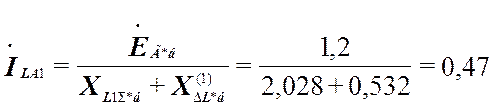 ;
;
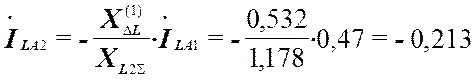 ;
;
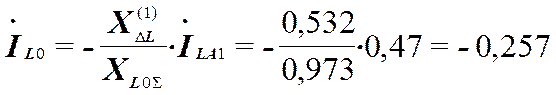 .
.
Для проверки правильности вычислений
определим ток фазы А (вместе разрыва): 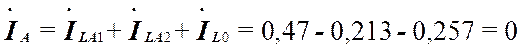 .
.
Значения токов в именованных единицах на шинах нагрузки при обрыве одной фазы: ILA1 = 0,47·1105 A = 520 A; ILA2 = -0,213·1105 A = -235 A;
IL0 = -0,257·1105 A = -284 A.
Токи неповрежденных фаз В и С у нагрузки:
![]() = a2·
IL1 +a ·IL1 + IL0 = (-0,5 – j0,867)·520 - (-0,5 + j0,867)·235 – 284 =
= a2·
IL1 +a ·IL1 + IL0 = (-0,5 – j0,867)·520 - (-0,5 + j0,867)·235 – 284 =
= - 260 – j450 + 118 – j204 – 284 = - 426 – j654 = 778 ![]() 236° A;
236° A;
![]() =
a · IL1 + a2 ·IL1 + IL0 = (-0,5 + j0,867)·520 - (-0,5 - j0,867)·235 – 284 =
=
a · IL1 + a2 ·IL1 + IL0 = (-0,5 + j0,867)·520 - (-0,5 - j0,867)·235 – 284 =
= -
426 + j654 = 778 ![]() 124° A;
124° A;
Определим напряжения в неполнофазном режиме:
а)
В месте обрыва: ![]() ;
;
![]() ;
;
![]() .
.
Как видим, граничные условия выполняются.
б) Напряжения на шинах нагрузки:
![]() ;
;
![]() ;
;
![]() .
.
Напряжения неповрежденных фаз В и С:
UBн = (-0,5
– j0,867)·0,72 ∙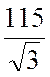 + (-0,5 + j0,867)·0,148·
+ (-0,5 + j0,867)·0,148·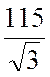 + 0,032·
+ 0,032·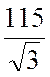 =
=
=
-24 – j41,6 – 5 + j8,66 + 2,14 = - 26,86 – j32,94
= 42 ![]() 232° кВ;
232° кВ;
UСн = (-0,5
+ j0,867)·0,72 ∙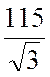 + (-0,5 - j0,867)·0,148·
+ (-0,5 - j0,867)·0,148·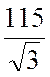 +
0,032·
+
0,032·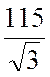 =
=
= -
26,86 + j32,94 = 42 ![]() 124° кВ.
124° кВ.
Мощность, передаваемая по фазам В и С в неполнофазном режиме:
Рнеп.(В и С) = 2∙42 кВ∙ 0,8 кА = 66 МВт.
3.23 Для схемы Рис.3.34 определить токи и напряжения в линии и на шинах нагрузки при обрыве двух фаз.
ГЛАВА 4 ОСОБЫЕ ВИДЫ ПЕРЕХОДНЫХ ПРОЦЕССОВ
Глава 4.1 Гашение электромагнитного поля синхронных машин
Основные расчетные соотношения:
§ ток возбуждения при гашении поля
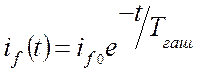 ,
, ![]() (4.1)
(4.1)
§ постоянная времени гашения магнитного поля
![]()
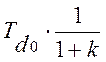 ,
,
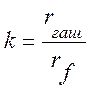 (4.2)
(4.2)
§ максимальное напряжение на обмотке возбуждения
![]() (4.3)
(4.3)
§ допустимое напряжение на обмотке возбуждения
![]() (4.4)
(4.4)
§ время гашения магнитного поля генератора
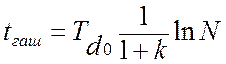 ,
,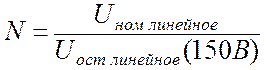 (4.5)
(4.5)
4.1 Синхронный генератор работает в режиме холостого
хода. Внезапно возникла необходимость снять возбуждение с машины. Определить
время, по истечении которого напряжение на выводах машины составит ![]() . Известно, что
. Известно, что ![]() ,
,
![]()
Решение:
Определяем постоянную гашения магнитного поля:
![]()
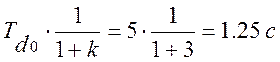
После чего может быть найдено требуемое время:
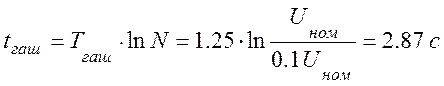
Итак, время, по прошествии, которого
напряжение на шинах генератора снизится до ![]() составляет 2.87 с
составляет 2.87 с
4.2 Синхронный генератор работает на холостом ходу, внезапно срабатывает автомат гашения поля (АГП), определить время, по истечении которого магнитное поле машины может считаться погашенным. Гашение осуществляется на постоянное активное сопротивление
Генератор ТВВ -200-2АУ3, ![]() ,
,
![]()
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
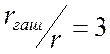
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.