Электромагнитные переходные процессы в электрических системах: Сборник задач для студентов электроэнергетических специальностей, страница 16

где n – число проводов в расщепленной фазе; r – радиус одиночного провода; а_ср – среднее геометрическое расстояние между проводами одной фазы; μ – относительная  магнитная проницаемость среды, для воздуха μ = 1.

          Сопротивление, обусловленное взаимоиндукцией между двумя петлями "провод-земля" с расстоянием d между осями их проводов (Рис. 3.4) определяется из выражения:

                            Х_М = 0,145·lg , Ом/км                                                       (3.6)

          Для трехфазной одноцепной линии с полным циклом транспозиции проводов сопротивление взаимоиндукции между фазами определяется по выражению:

                                                 Х_{М ср} = 0,145·lg, Ом/км                              (3.7)

где D_ср = ,  – среднее геометрическое расстояние между проводами фаз А, В, С.

          Индуктивное сопротивление прямой (обратной) последовательности  

                                                          Х₁ = Х₂ = Х_L – X_Мср                                  (3.8)

 Подстановка (3.4) и (3.7) в (3.8) даёт формулу для расчета сопротивлений прямой и обратной последовательности ЛЭП:

                                              Х₁ = Х₂ = 0,145·lg , Ом/км ,                        (3.9)

которое для линии длиной 1 км приводится в справочниках (см. Глава 1).                

          Активные сопротивления линии "провод-земля" складываются из активного сопротивления провода r_п и дополнительного сопротивления r_з, учитывающего потерю активной мощности в земле от протекающего в ней тока, т.е.                                

                                                r = r_п + r_з                                                                                       (3.10)                                               

Сопротивление                    r_з = π²·f·10^-4 Ом/км,                                           (3.11)                                      

которое при f = 50 Гц дает r_з = 0,05 Ом/км. Зная Х_L и Х_Мср нетрудно найти сопротивление нулевой последовательности одноцепной трехфазной линии

                               Х₀ = Х_L +2·Х_Мср = 0,435·lg , Ом/км                           (3.12)

где                                                  r_ср =                                             (3.13)

средний геометрический радиус системы трех проводов линии.

          В то время, как при токе прямой (обратной) последовательности  взаимоиндукция с другими фазами уменьшает сопротивление фазы, при токах нулевой последовательности она увеличивает его. Токи нулевой последовательности, протекающие в тросах ЛЭП,  оказывают размагничивающее действие, что приводит к некоторому уменьшению результирующего потокосцепления фазы. В зависимости от материала троса они оказывают разное влияние на уменьшение индуктивного сопротивления нулевой последовательности линии. В таблице 3.1 приведены эти соотношения.

Таблица 3.1

Средние значения соотношений между Х₀ и Х₁ для воздушных линий передачи

Характеристика линии	Отношение Х0/Х1
Одноцепная линия без тросов То же со стальными тросами То же с хорошо проводимыми тросами Двухцепная линия без тросов То же со стальными тросами То же с хорошо проводимыми тросами	3,5 3,0 2,0 5,5 4,7 3,5

5. Кабели.

Активные и индуктивные сопротивления прямой (обратной) последовательности кабеля можно определить так же, как и для воздушных линий, используя уравнение (12).

В ориентировочных расчетах, для трехжильных кабелей, сопротивления нулевой последовательности обычно принимают:

                                 r₀ ≈ 10∙r₁;   X₀ = (0,35 ÷ 4,6)∙Х₁                                 (3.14)      

3.1 Определить индуктивные сопротивления прямой, обратной и нулевой последовательности линии 110 кВ, выполненной проводом АС-95.

Расстояние между фазами d_АВ = 4,06 м; d_АС = 3,5 м; d_ВС = 3,09 м. Радиус провода r = 6,75∙10^-10 м.

Среднегеометрическое расстояние Среднегеометрическое расстояние между фазами

D_ср =  м.

                                                           Решение

 Удельное индуктивное сопротивление линии «провод-земля»

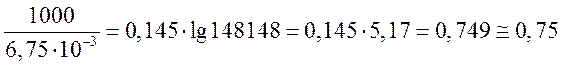Х_L = 0,145∙lg = 0,145∙lgОм/км

Для трехфазной линии

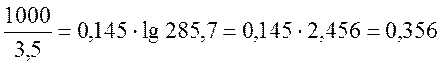Х_Мф = 0,145lg = 0,145∙lg Ом/км

Сопротивление прямой (обратной) последовательности

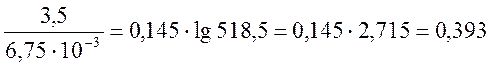Х₁ = 0,145lg = 0,145∙lg Ом/км

Х₂ = Х₁ = Х_L – Х_М

Проверка

Х_L =  Х₁ + Х_М = 0,393 + 356 = 0,7496 ≈ 0,75 Ом/км

Удельное сопротивление нулевой последовательности линии

Х₀ =  Х_L + 2∙Х_М = 0,7496 + 2∙356 = 1,461 ≈ 0,75 Ом/км

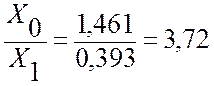 (по табл. 2 )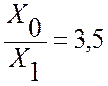

3.2 Определить полные сопротивления прямой, обратной и нулевой последовательности линии 220 кВ, выполненной проводом АС-240.

Расстояние между фазами d_АВ = 7,5 м; d_AC = 15 м; d_ВC = 7,5 м.

Радиус провода r = 1,53 см.

Удельное активное сопротивление провода r_уд = 0,064 Ом/км.

 Ответ.  Удельные параметры ЛЭП-220 кВ: Z_l=0.144+j0.711oм/kм; Z_m=0.05+j0.293 oм/kм;

 По удельным параметрам определяются Z_1, Z₂     и   Z_0.

3.2. Расчет токов несимметричных коротких замыканий.

Расчеты могут проводиться методом фазных координат и с применением метода симметричных составляющих.

          При использовании метода симметричных составляющих абсолютная величина тока при любом виде несимметричных К.З. пропорциональна  току прямой последовательности в месте К.З. и может быть определена из следующего общего выражения [1]:

1)  В именованных единицах

;

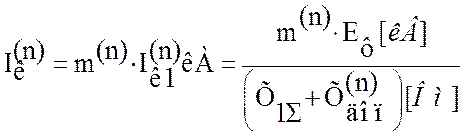где n – вид к.з./1ф – 1; 2ф – 2; 2ф на землю – 1,1); Е_ф [kB]= E_л [kB]/

2)  В относительных базисных единицах

,

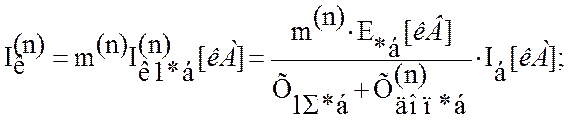где – m⁽ⁿ⁾ - коэффициент пропорциональности, зависящий от вида К.З., учитывает участие токов обратной и нулевой последовательности в полном токе К.З.,

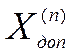 - дополнительное индуктивное сопротивление, вводимое в схему прямой последовательности, величина которого зависит от вида К.З. и определяется только значениями Х_2Е и Х_0E, соответственно в именованных  или относительных единицах.